Basic! 인공지능 수학 네번째 시간으로 벡터의 투영과 직교분해에 대해 배워보도록 합시다.
투영(projection)
내적
두 벡터 $u$와 $v$에 대한 내적은 다음과 같이 정의됩니다.
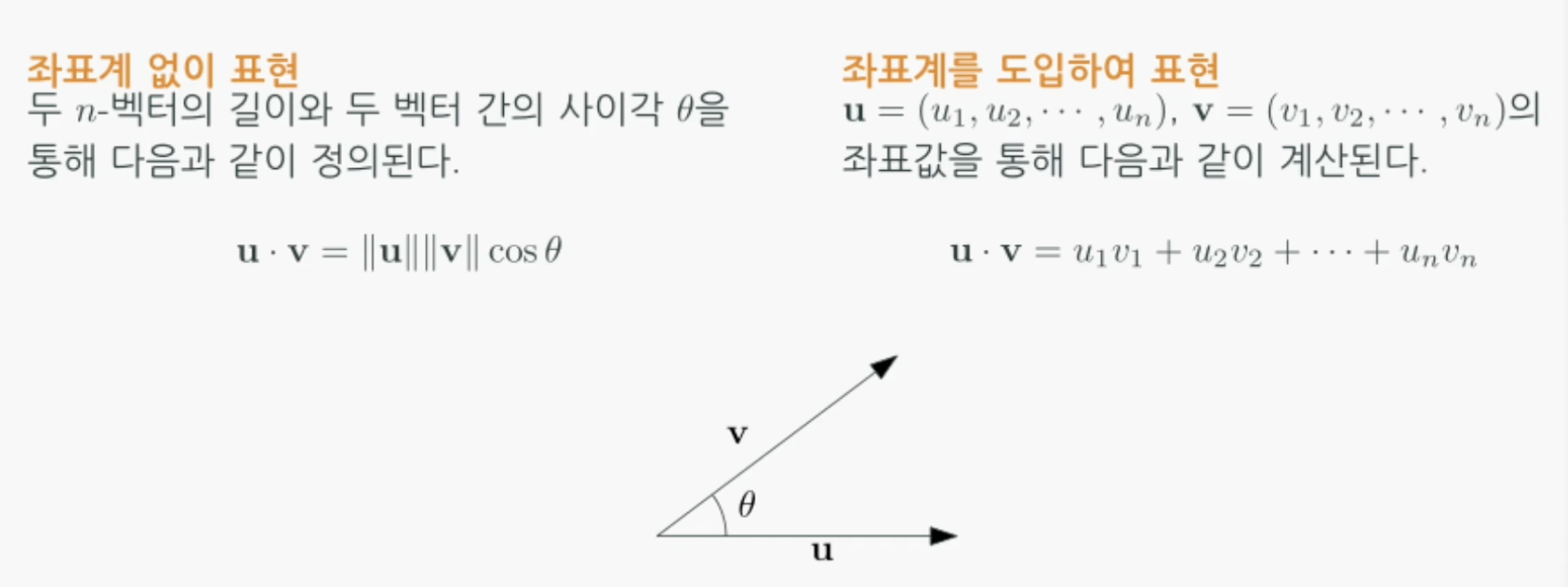
두 벡터 $u$,$v$ 간의 내적이 0이면 두 벡터는 직교(orthogonal)합니다.

투영(projection)

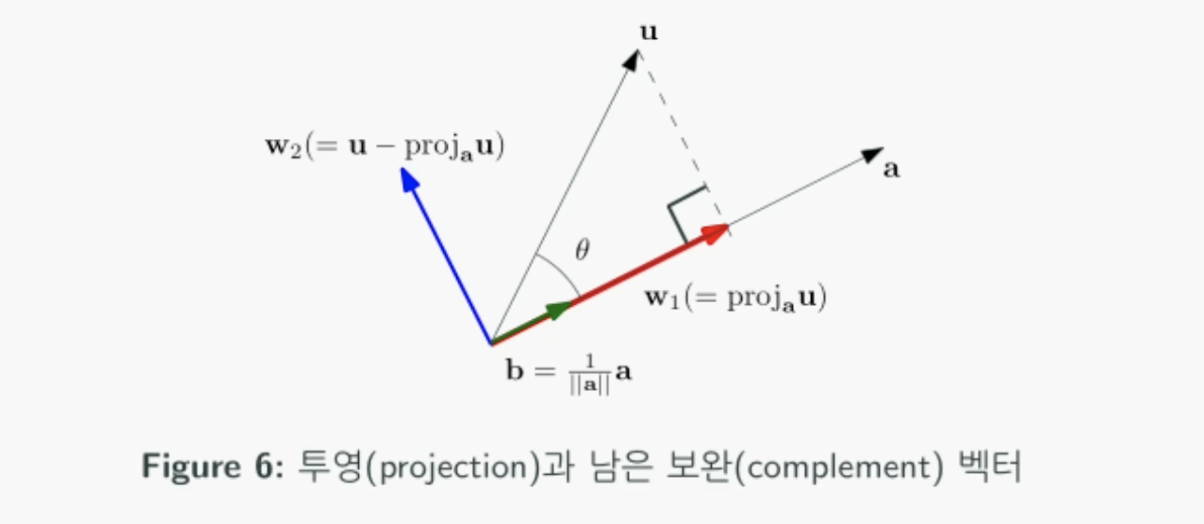
여기서 중요한 점은 투영한 벡터와 보완 벡터는 서로 직교(orthogonal)하다는 것입니다.
두 벡터 $u$,$a$가 있을 때, 투영과 보완의 개념을 이용해 직교분할을 할 수 있습니다.
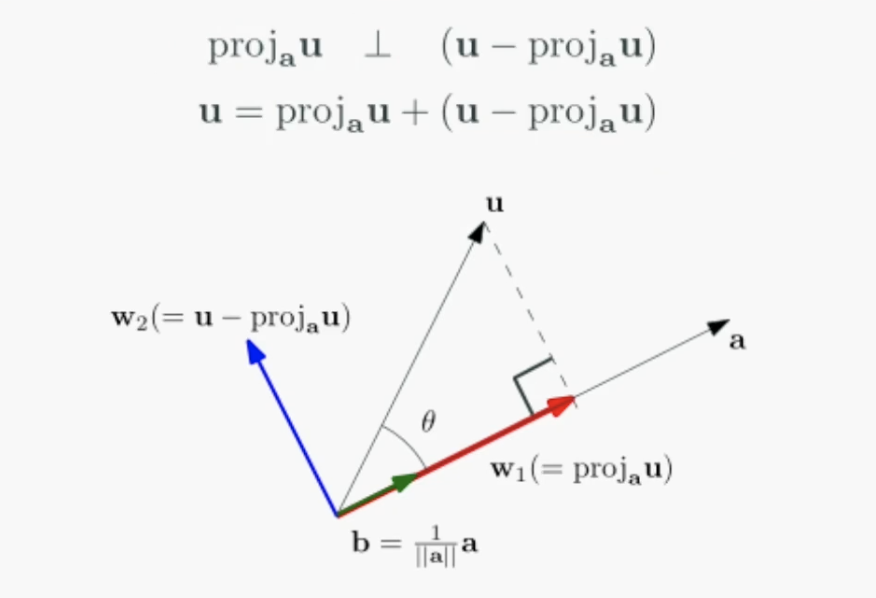
직교행렬(Orthogonal Matrix)
직교행렬을 구한다는 것은 직교좌표계를 구한다는 것과 같습니다.
직교좌표계를 이용하면 어떤 장점이 있는지 알아봅시다.
직교행렬
행렬은 각 열벡터가 기저를 이루는 좌표계입니다.
주어진 행렬의 모든 열벡터가 서로 직교한다면, 이 행렬을 직교행렬이라 합니다.
직교행렬은 직교좌표계를 의미합니다.
위와 같이 주어진 행렬이 직교행렬이고 모든 열벡터의 크기가 1이라면
이 행렬을 정규 직교행렬(orthonormal matrix)이라 합니다.
정규직교행렬은 정규직교좌표계를 의미합니다.
직교행렬을 이용한 선형시스템

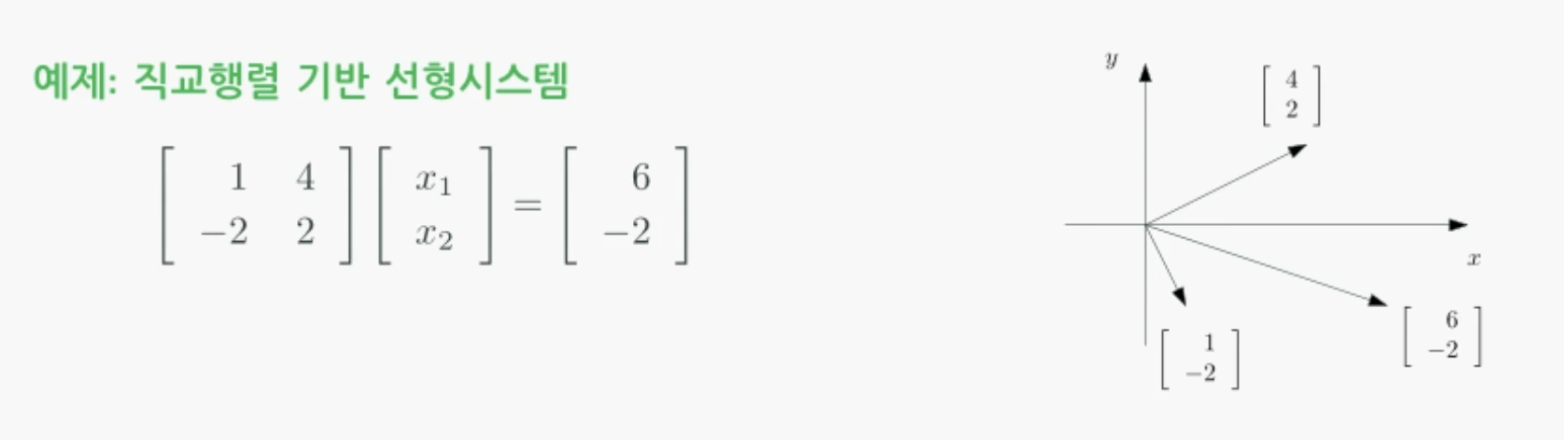
정규직교행렬을 이용한 선형시스템

QR 분해: A = QR
주어진 행렬에서 정규직교행렬을 추출하면 (그람-슈미트 과정)
직교행렬을 이용한 선형시스템 계산의 효율성을 누릴 수 있습니다.
$n X n$ 정방행렬을 분해할 수 있습니다.
QR 분해
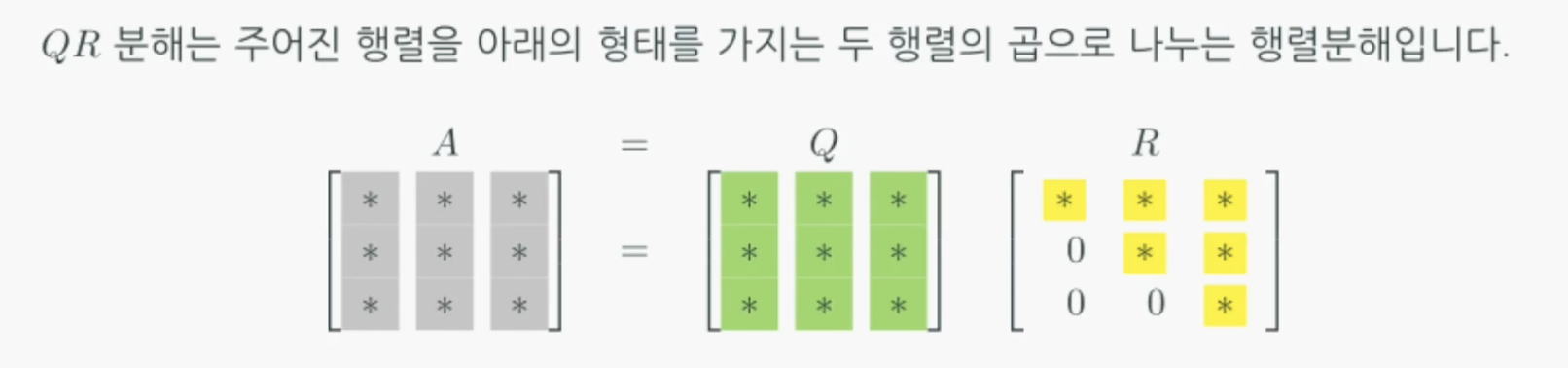
행렬 $Q$와 $R$은 그 특성에 따라 다음과 같이 불립니다.
- $Q$: orthonomal matrix(정규직교행렬)
- $U$: upper triangular matrix(상삼각행렬)
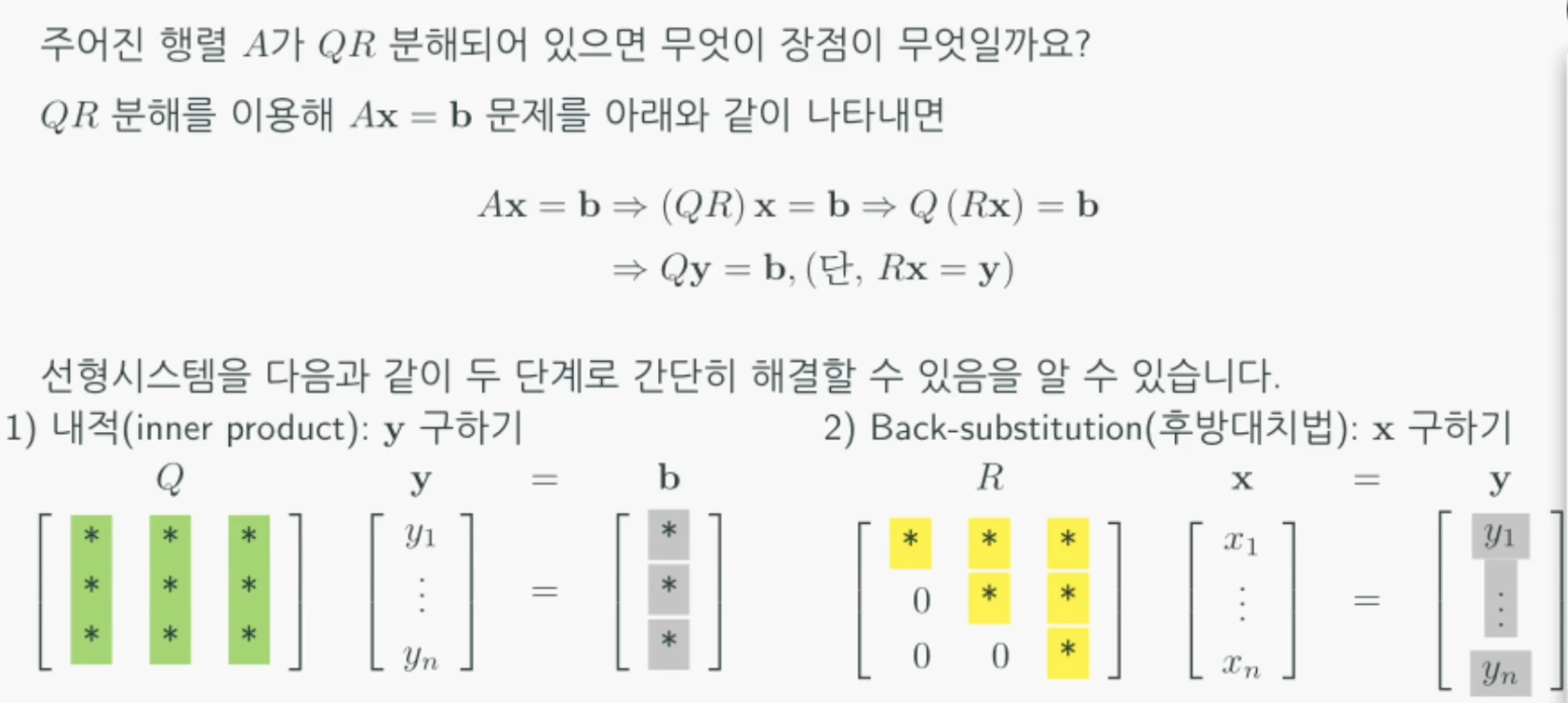
QR 분해의 활용
QR 분해는 다음의 이유로 활용됩니다.
- 빠른 계산: 선형시스템 $Ax = b$의 해를 구할 때, 정규직교행렬 $Q$를 이용한 계산 부분은 병렬처리로 빠르게 계산할 수 있습니다.
그러나 $R$을 이용한 계산 부분은 병렬처리 할 수 없습니다. - $b$가 자주 업데이트 되는 경우: 선형 시스템 $Ax = b$에서 행렬 $A$는 고정되어 있고 $b$가 자주 변하는 문제가 종종 있습니다.
이런 경우 행렬 $A$를 미리 QR로 분해해 둔다면, 선형시스템의 해 $x$를 실시간으로 구할 수 있습니다.

댓글남기기