Basic! 인공지능 수학 part 10: 추정

Basic! 인공지능 수학 열 번째 시간으로 표본분포에 대해 알아보도록 합시다.

 

 

추정

 

모평균의 추정

 

• 점추정

  저번 시간에 표본의 평균이 대략적으로 모평균을 따라간다는 것을 알 수 있었습니다.

  따라서 모평균의 추정은 다음과 같습니다.

    import numpy as np
    samples = [9, 4, 0, 8, 1, 3, 7, 8, 4, 2]
    print(np.mean(samples))
  

 

• 구간추정

  추정하려는 값을 몇 % 신뢰할 수 있는지 신뢰구간을 제시해서
  타당성을 부여합니다.

  

  표본의 크기가 30개 이상이면 중심극한 정리를 사용할 수 있습니다.
  이 경우에 표본표준편차를 사용할 수 있습니다.

  

  문제 1
  
  

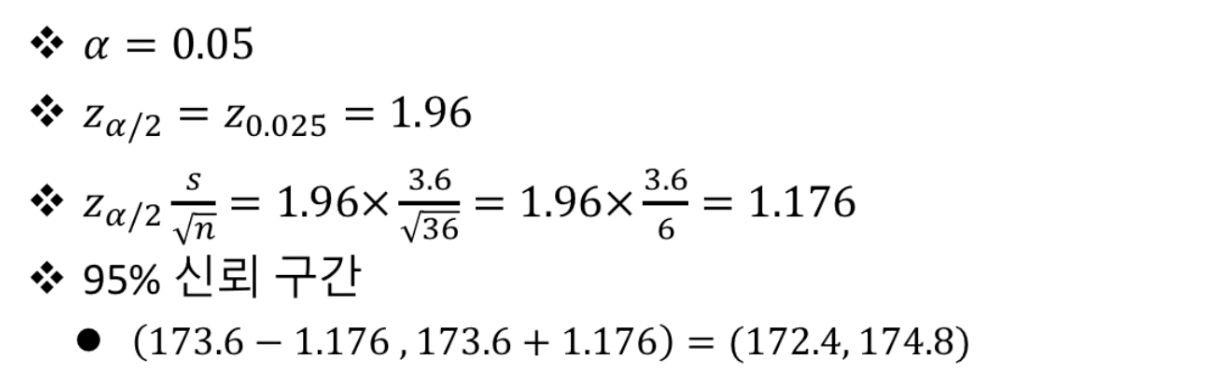
  문제 2
  

    import numpy as np
      
    w = [10.7, 11.7, 9.8, 11.4, 10.8, 9.9, 10.1, 8.8, 12.2, 11.0, 11.3, 11.1, 10.3, 10.0, 9.9, 11.1, 11.7, 11.5, 9.1, 10.3, 8.6, 12.1, 10.0, 13.0, 9.2, 9.8, 9.3, 9.4, 9.6, 9.2]
  
    xbar = np.mean(w)
    # 표본표준편차의 자유도는 n-1이기 때문에
    # ddof에는 1을 넣어줍니다. 
    sd = np.std(w,ddof=1)
    print("평균: %.2f, 표준편차: %.2f", %(xbar, sd))
  
    import scipy.stats
      
    alpha = 0.05
    zalpha = scipy.stats.norm.ppf(1-alpha/2)
    print("zalpha: ",zalpha)
  

  위 코드는 다음과 같습니다.

  

 

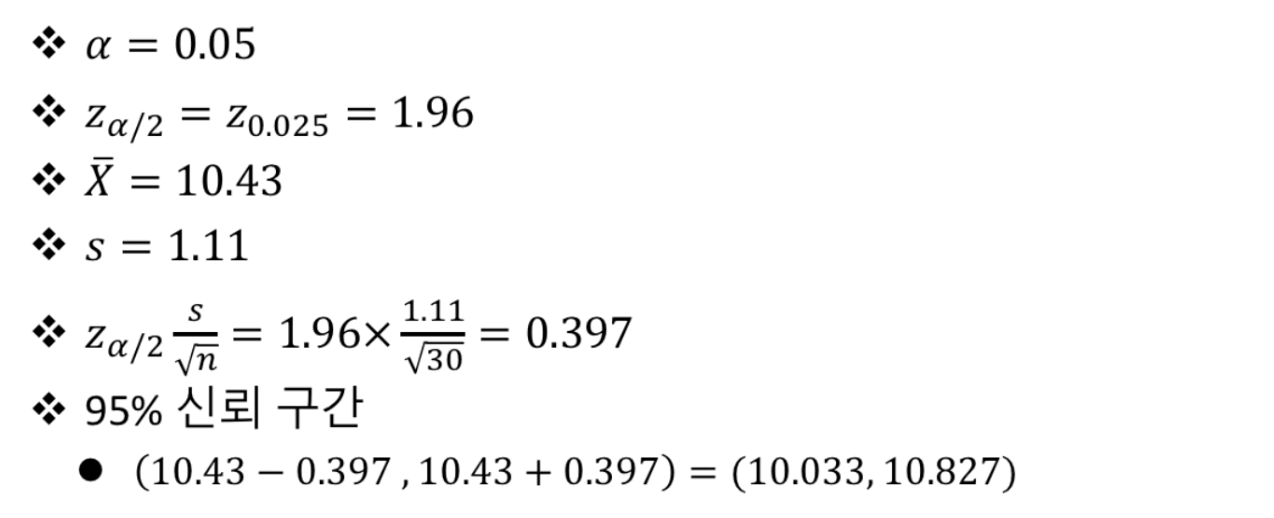
모비율의 추정

 

• 점 추정

  

  문제 1
  

 

• 구간 추정

  

  

  문제 1

  

  

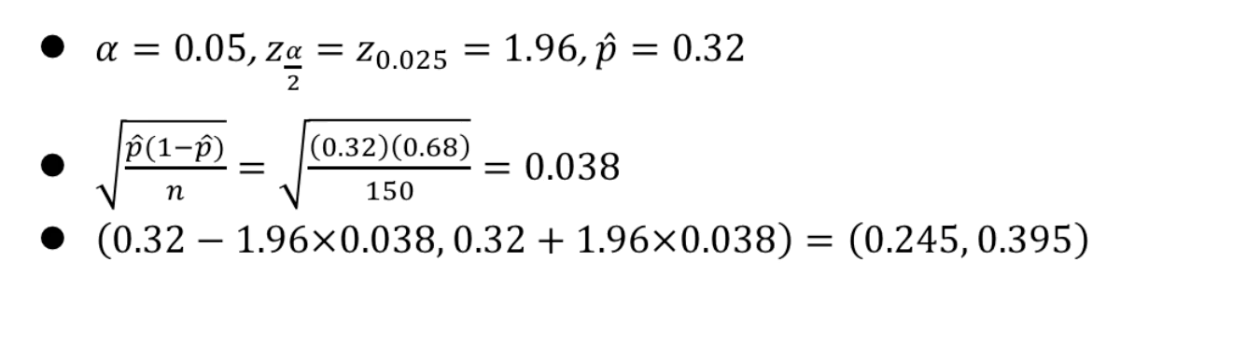
    import numpy as np
      
    x = 48
    n = 150
    phat = x / n
    alpha = 0.05
      
    zalpha = scipy.stats.norm.ppf(1-alpha/2)
    sd = np.sqrt(phat*(1 - phat)/n)
    print("phat: %.3f, zalpha: %.3f, sd: %.3f" %(phat, zalpha, sd))
  
    ci = [phat - zalpha * sd, phat + zalpha * sd]
    print(ci)