Basic! 인공지능 수학 part 5: 최소제곱법

Basic! 인공지능 수학 다섯 번째 시간으로 최소제곱법에 대해 알아보도록 합시다.

집합과 공간

집합(set)은 임의의 원소(element)를 수집하여 만든 모음입니다.

집합이 연산에 닫혀 있다는 개념이 있습니다.
어떤 연산을 생각한 다음, 집합에서 임의의 원소를 뽑아 연산을 수행한 결과가
여전히 집합의 원소로 있다면, 해당 집합은 연산에 닫혀 있다고 합니다.
다음 집합은 덧셈연 산에 닫혀 있지 않습니다. 하지만 곱셈 연산에는 닫혀 있습니다.

\[\{-1, 0, 1\}\]

Column Space (열공간)

행렬 A의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성할 수 있을 것입니다. 이러한 집합을 column space (열공간)이라 하고 다음과 같이 표기합니다. \(col\(A\)\)

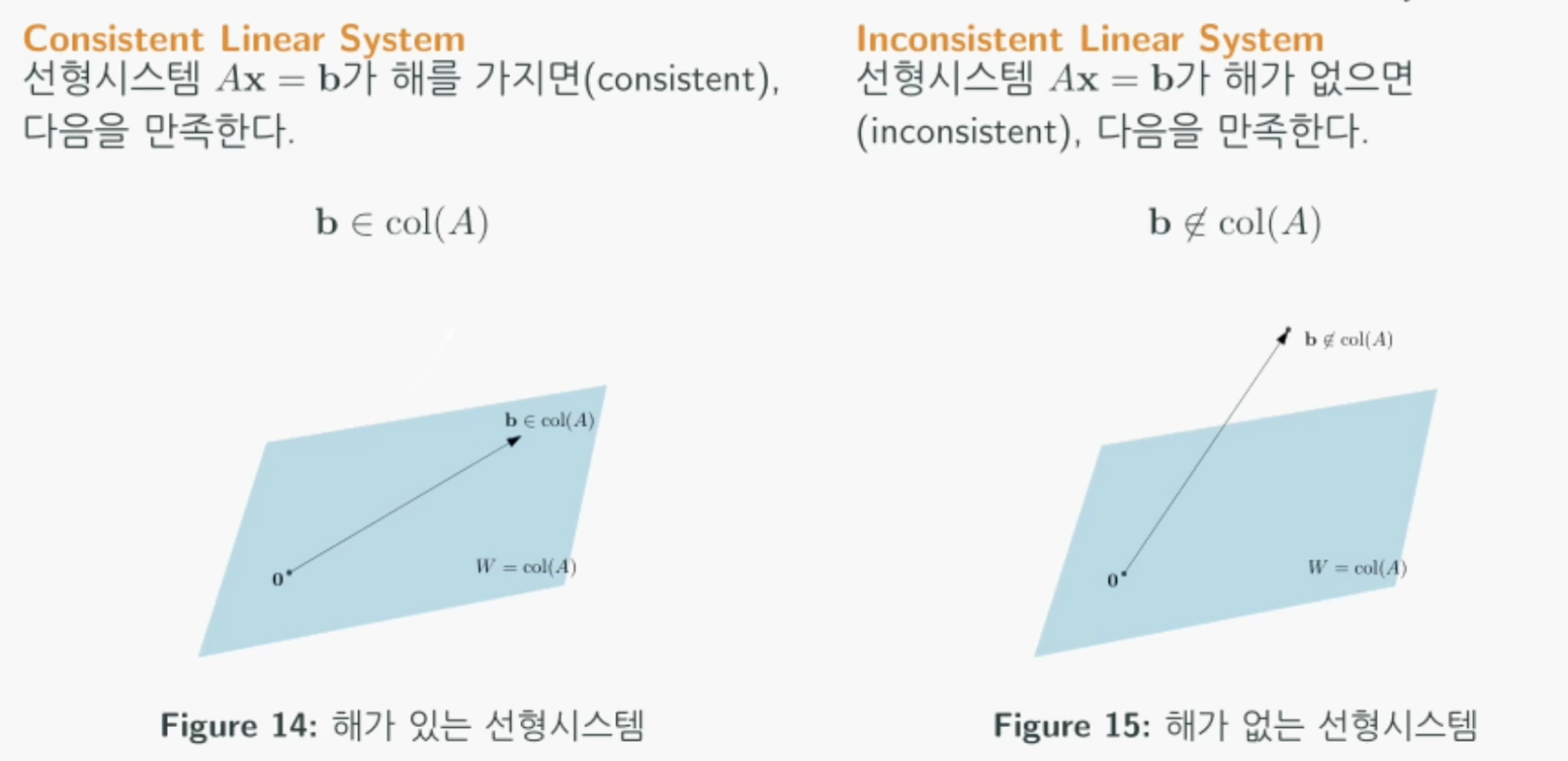
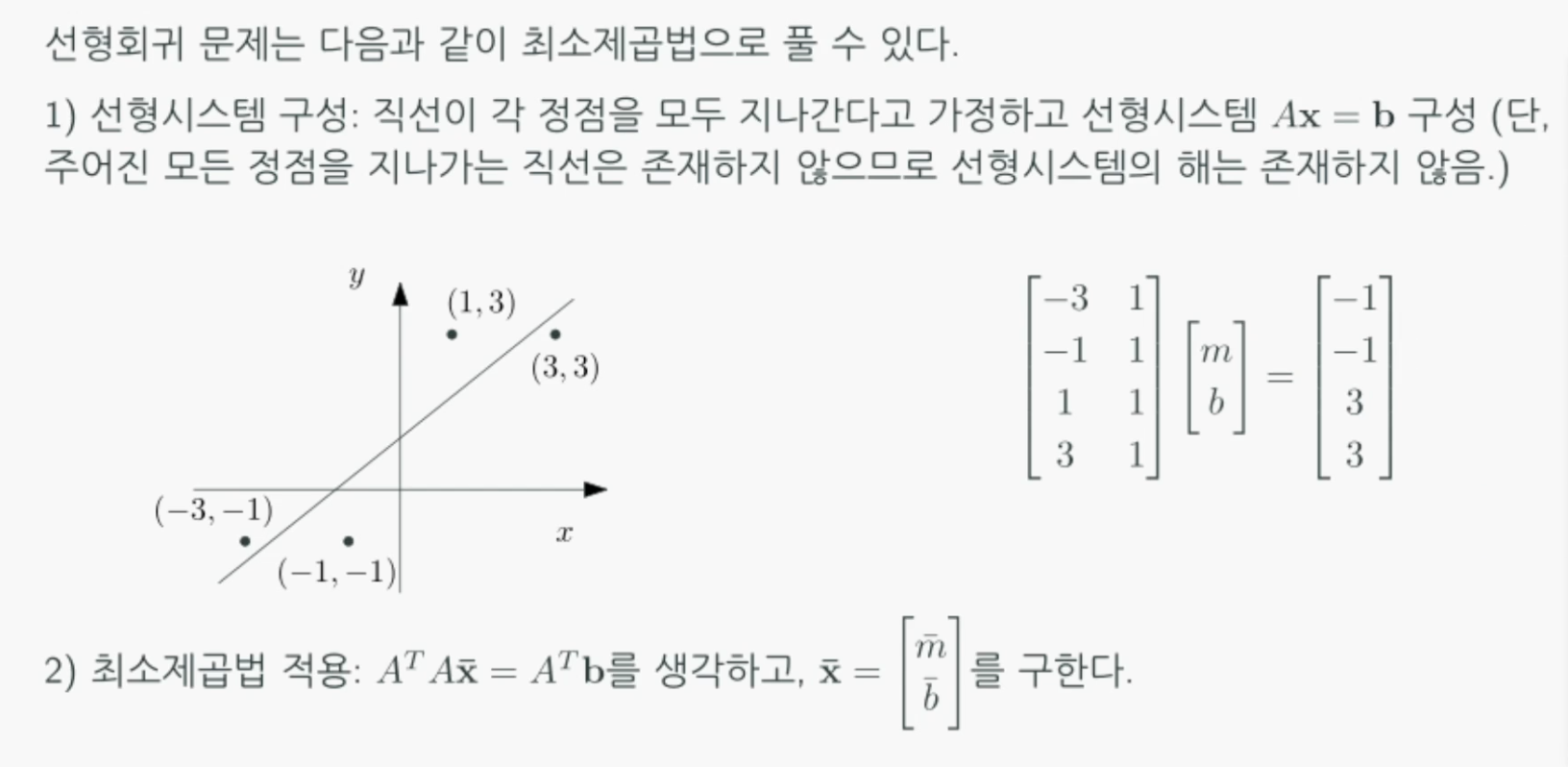
최고제곱법 (least squares method)

선형시스템 $Ax = b$에 대한 해가 없음에도 불구하고, 우리가 할 수 있는 최선이 무엇인지 알고 싶을 때 사용하는 방법입니다.

행렬 $A$가 정의하는 열공간에서 목표 $b$와 가장 가까운 지점은 b를 열공간에 투영한 점일 것입니다.
즉, 달성가능한 최선의 목표 $proj_wb$를 생각해 볼 수 있습니다.

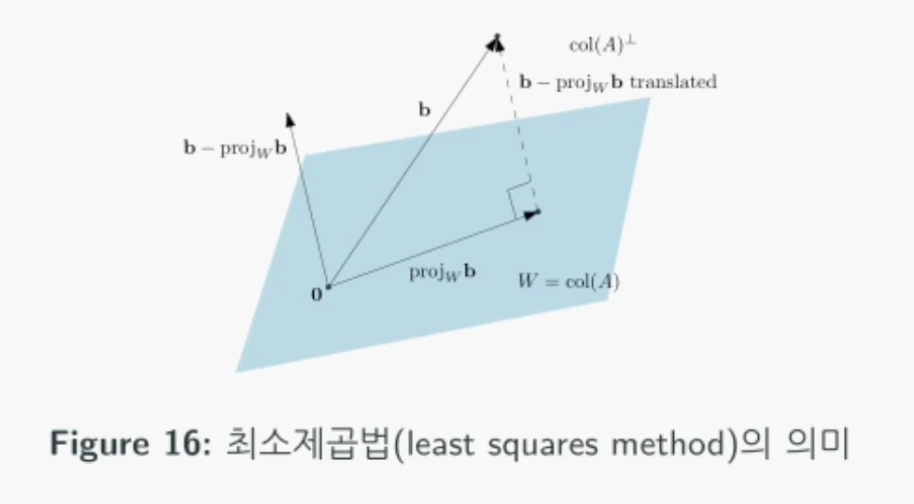
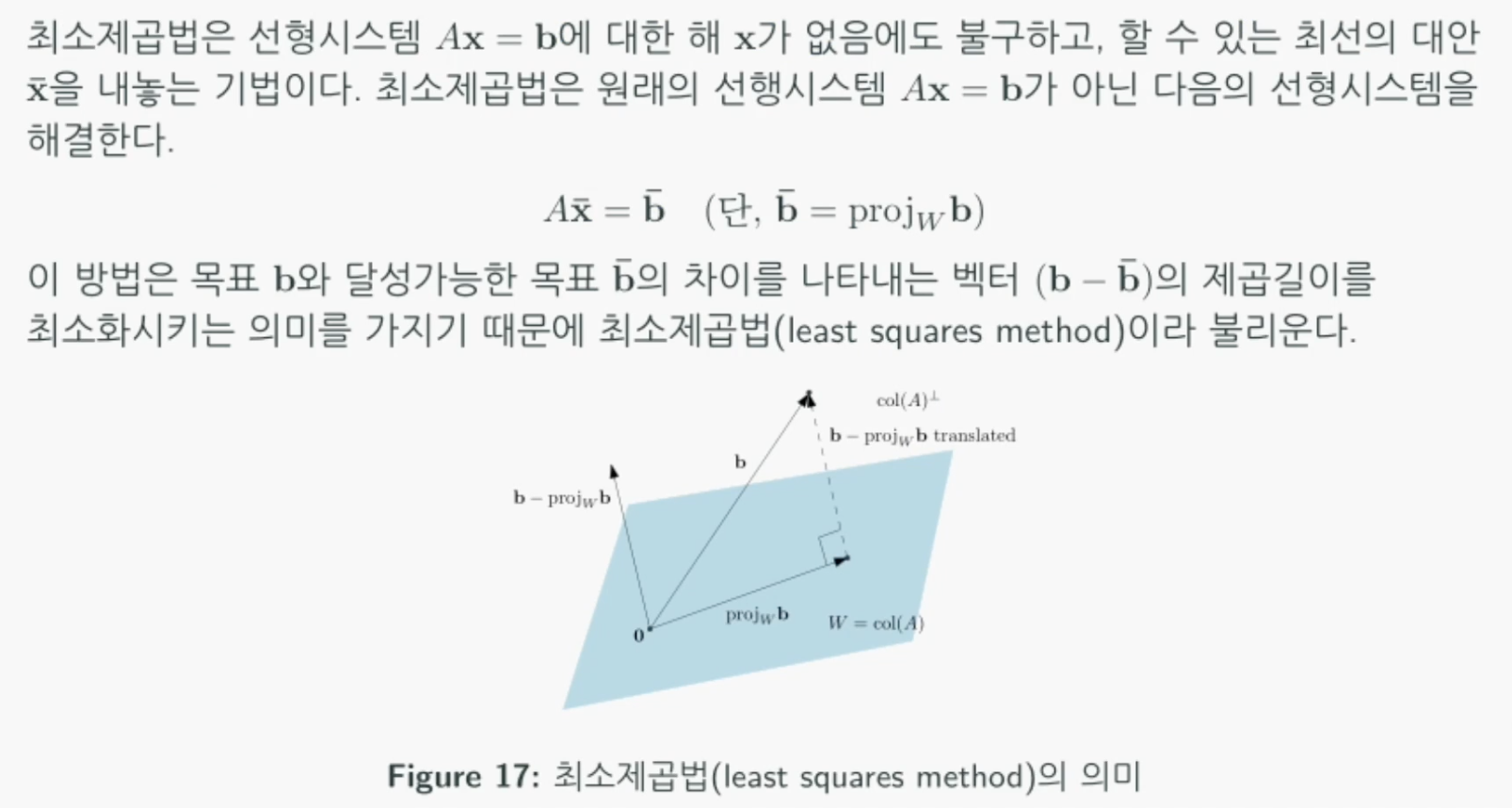
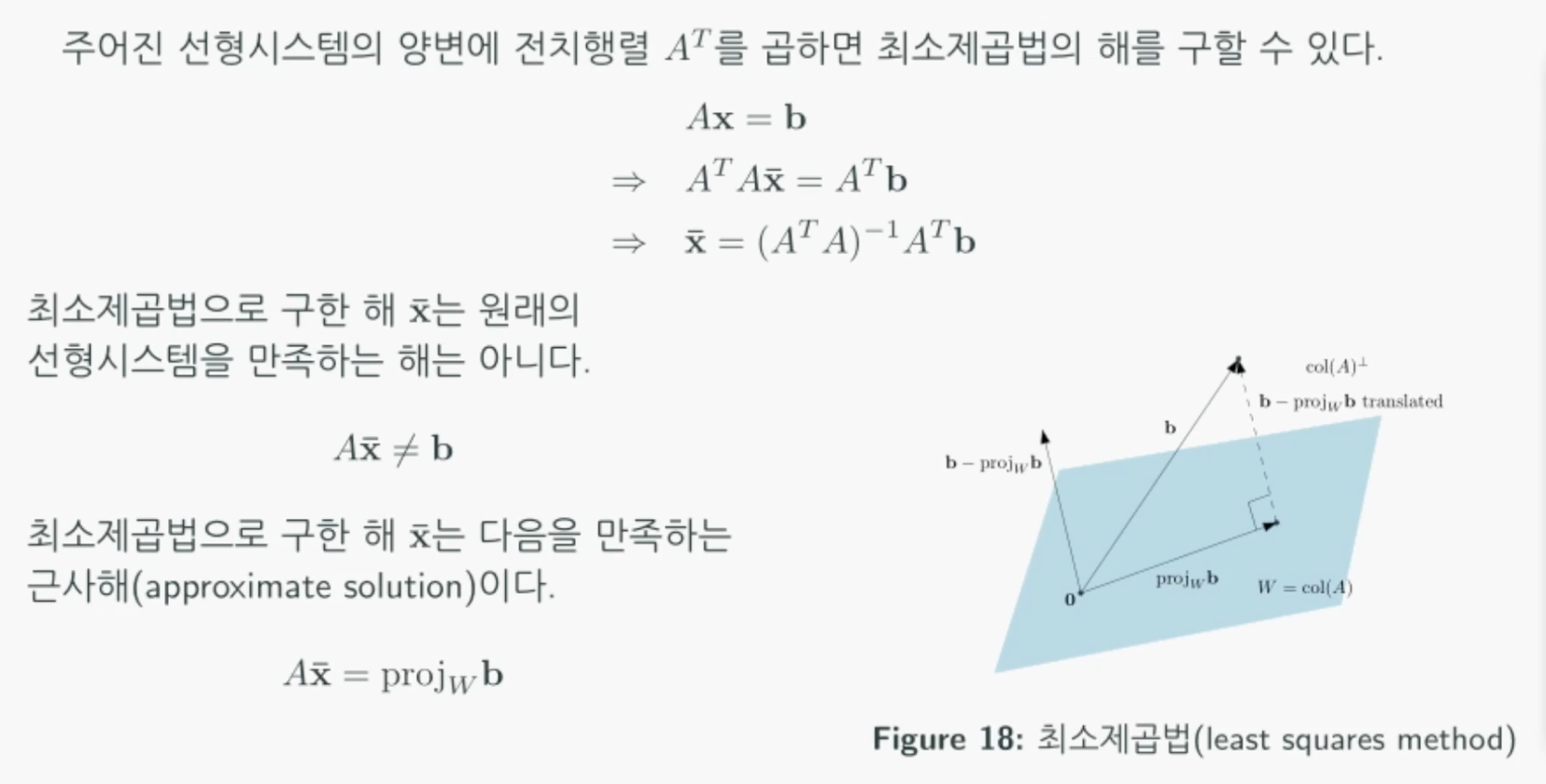
최소제곱법의 응용: 선형회귀(Linear Regression)