Basic! 인공지능 수학 part 8: 확률분포

Basic! 인공지능 수학 여덟 번째 시간으로 확률분포에 대해 알아보도록 합시다.

학률분포

확률 변수 (random variable)

랜덤한 실험 결과에 의존하는 실수를 의미합니다.
즉, 표본 공간의 부분 집합에 대응하는 실수를 의미합니다.
보통 표본공간에서 실수로 대응되는 함수로 정의합니다.
X나 Y같은 대문자로 표시됩니다.

• 이산확률변수 (discrete random variable) 확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우
• 연속확률변수 셀 수 없는 경우

확률분포 (Probability Distribution)

확률변수가 가질 수 있는 값에 대해 확률을 대응시켜주는 관계를 말합니다.

이산확률변수의 확률분포

보통함수로 주어지며, 확률변수 X가 x라는 값을 가질 확률을 의미합니다.
\(P(X = x) = f(x)\)

이산확률변수의 평균

기대값이라고도 합니다. 평균적으로 기대할 수 있는 수치이기 때문입니다.
\(E(X) = \Sigma_xxP(X = x) = \Sigma_xxf(x)\)

이산확률변수의 분산

실험을 할 때마다 확률변수의 값이 달라질 수 있습니다.
이 변동의 정도인 분산을 계산해 볼 수 있습니다.
$(X-\mu)^2$의 평균입니다.

\[\sigma^2 = E[(X-\mu)^2] = \Sigma_x(X-\mu)^2P(X=x)\]

분산의 식을 정리해주면 다음과 같이 나타낼 수 있습니다.

\[E(X^2) - \{E(X)\}^2\]

결합확률 분포 (joint probability distribution)

두 개 이상의 확률 변수가 동시에 취하는 값들에 대해 확률을 대응시켜주는 관계를 나타냅니다.

공분산

분포의 경향을 볼 때 사용합니다.

\[Cov(X,Y) = E[XY] - E[X]E[Y]\]

상관계수 (correlation coefficient)

공분산은 각 확률 변수의 절대적인 크기에 영향을 받습니다.
단위에 의한 영향을 없애기 위해 다음과 같이 계산합니다.

\[Corr(X,Y) = \frac{Cov(X,Y)}{\sigma_X\sigma_Y}\]

몇가지 특별한 확률분포

이항분포

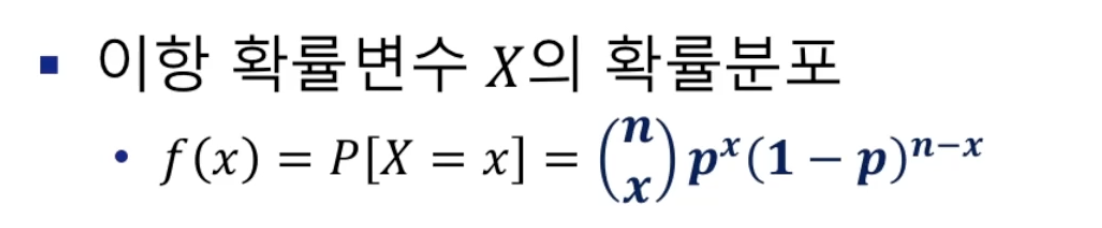
위 문제에서 등호가 포함되는지 안되는지는 아주 중요합니다!
cdf는 $-\infty$보다 크고 주어진 값보다 작은 확률을 구할 때 사용합니다.
(‘{}보다 작거나 같은 값’에서 {}, 베르누이 시행횟수, 확률 p)를 파라미터로 받습니다.

아래 코드는 평균과 분산을 각각 리턴합니다.

정규분포

지금까지 본 분포는 모두 이산확률분포였습니다.
이제 연속적인 확률 변수의 분포를 살펴봅시다.

정규분포는 확률 밀도 함수가 다음과 같이 생겼습니다.

\[f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2}\]

$\mu$와 $\sigma$가 정규분포의 모양을 결정합니다.
평균이 0이고 표준편차가 1이면 표준 정규분포라 합니다.

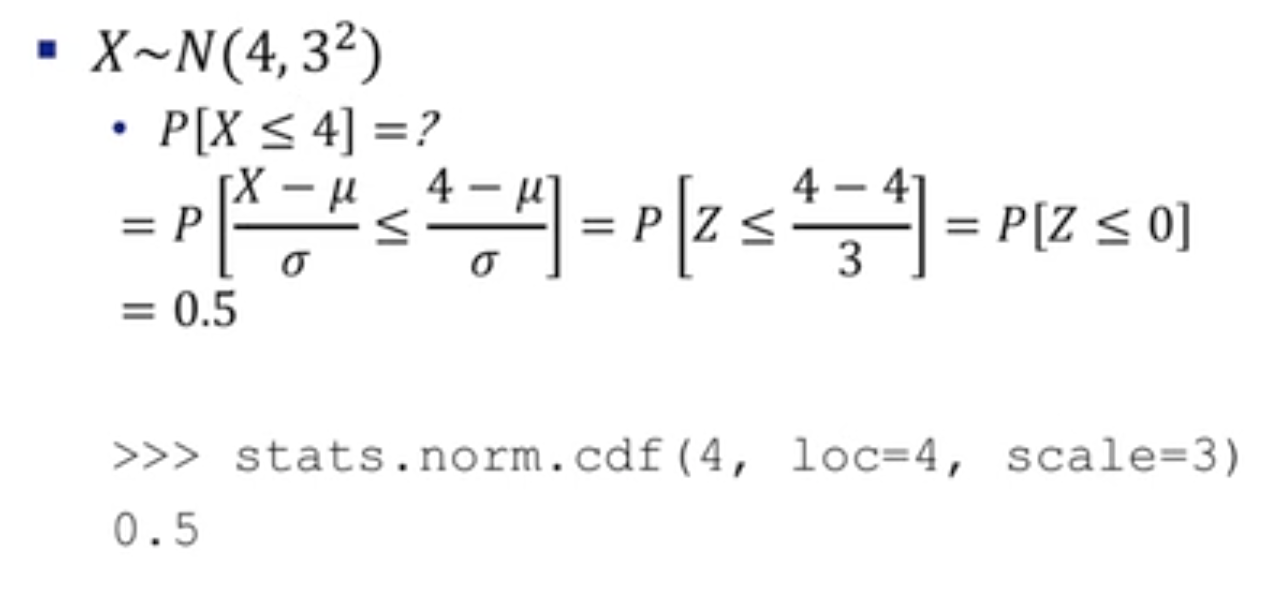
포아송 분포 (poisson distribution)

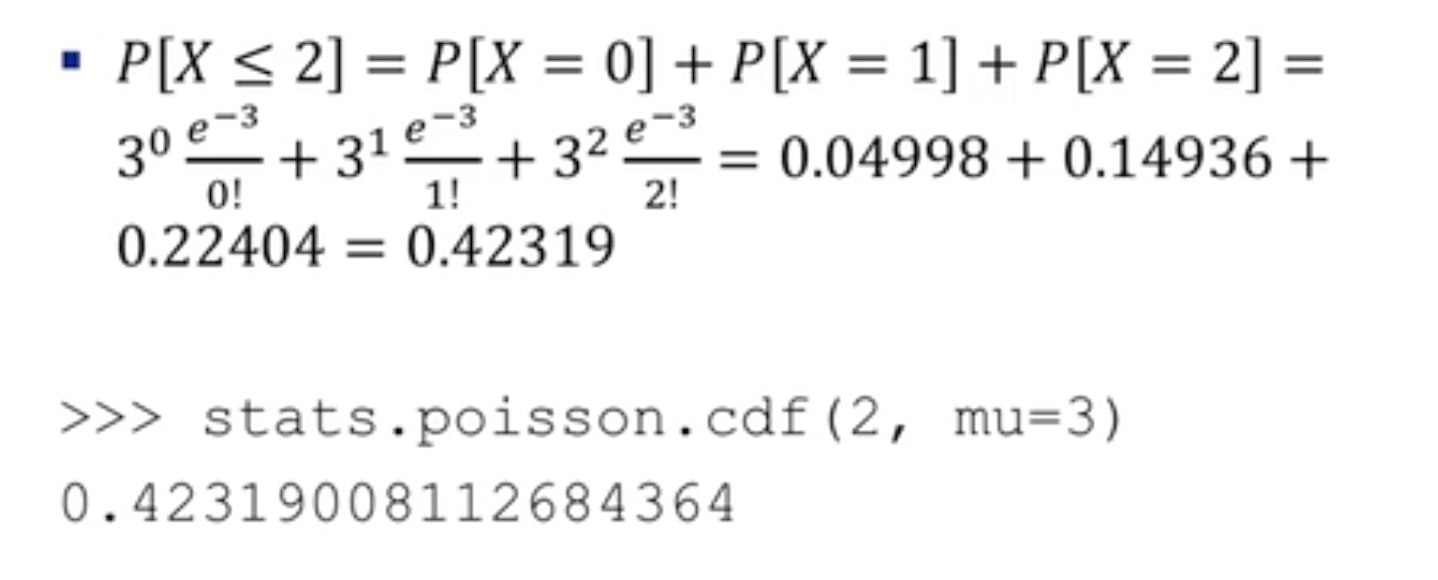
지수분포 (exponential distribution)