Basic! 인공지능 수학의 두번째 시간으로 행렬분해와 행렬연산에 대해 알아봅시다.
행렬분해
행렬분해의 의미 (matrix decomposition)
인수분해의 행렬버전이라 생각할 수 있습니다.
숫자의 인수분해는 주어진 숫자 (예: 12)를 여러 숫자의 곱으로 분해(예: 3 x 4) 하여 표현하는 것입니다.
인수분해는 어떤 경우에 쓸모가 있었나요?
- 분수의 약분
- 두 수의 최대공약수 구하기
- 두 수의 최소공배수 구하기
즉, 주어진 숫자를 인수분해 한 상태로 가지고 있으면 여러모로 계산이 편한 경우가 많습니다.
이 아이디어를 행렬에 도입한게 행렬분해라고 할 수 있습니다.
다음은 대표적인 행렬분해입니다.
- LU 분해 (LU decomposition)
- QR 분해 (QR decomposition)
- 특이값 분해 (SVD, Singular Value Decomposition)
이 포스트에서는 우선 LU 분해에 대해 알아보도록 하겠습니다.
LU 분해는 앞서 살펴본 가우스 소거법을 행렬에 적용시킨 것 입니다.
LU분해
가우스 소거법을 알고리즘의 형태가 아닌 행렬의 결과물로 표현하는 방식입니다.
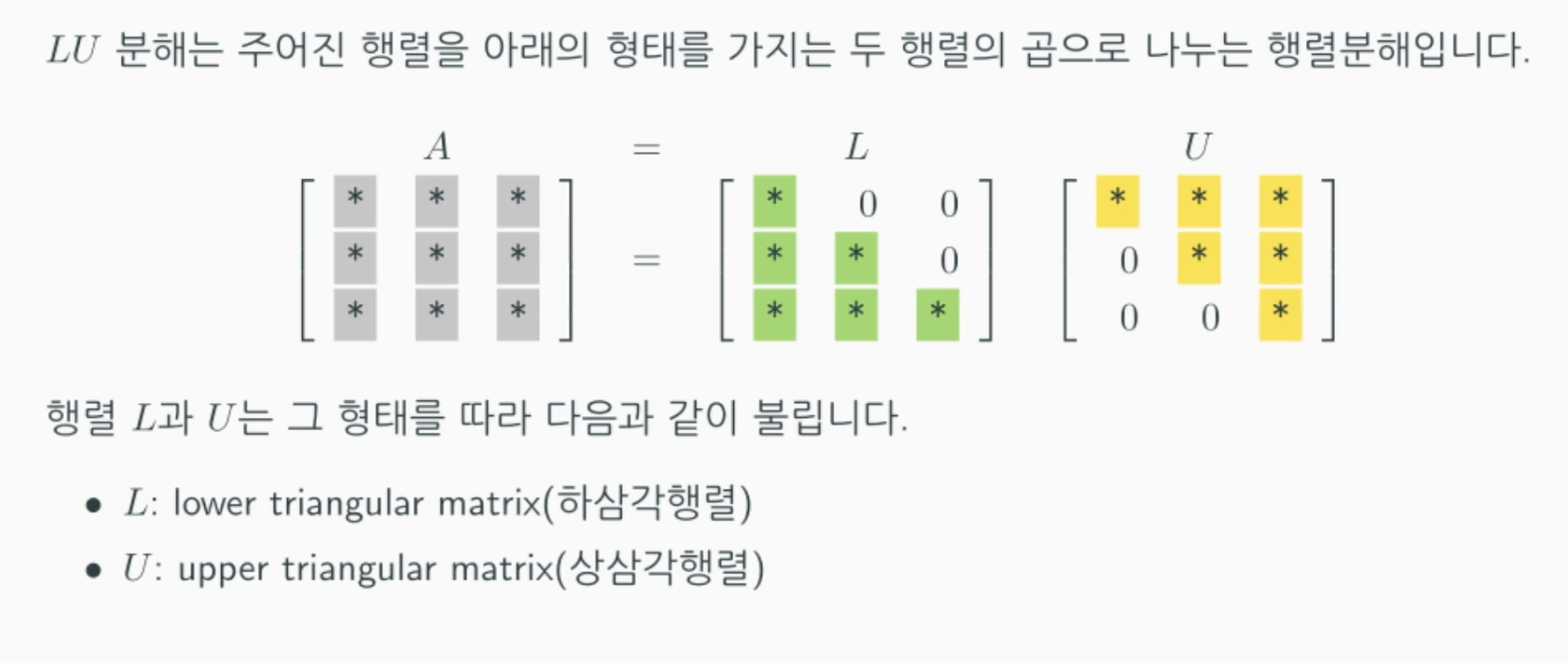
L은 우상단이 모두 0으로 이뤄져 있고 U는 좌하단이 모두 0으로 이뤄져 있는 행렬입니다.
주어진 행렬 $A$가 LU 분해되어 있으면 어떤 장점이 있을까요?
LU 분해를 이용해 $Ax = b$ 문제를 아래와 같이 나타내면
하나의 문제를 두개의 작은 문제로 쪼갤 수 있습니다.
\(Ax = b \rightarrow (LU) x = b \rightarrow L(Ux) = b\)
$\rightarrow Ly = b$, (단, $Ux = y$)
$Ly = b$ 를 통해 $y$를 구한후, $Ux = y$를 이용해 $x$를 구하면 됩니다. 앞서 배운 가우스 소거법을 이용해 해를 구하는 방식과 아주 유사합니다.
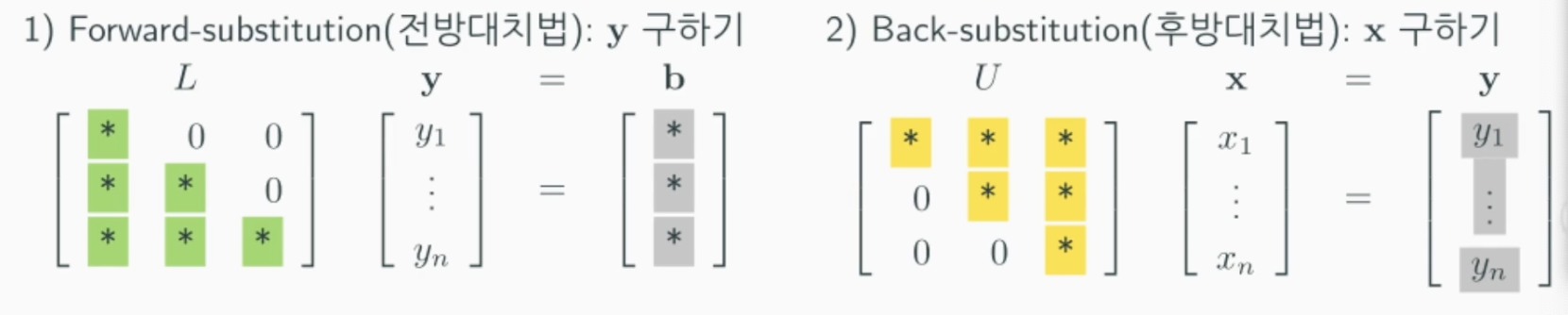
LU 분해는 가우스 소거법의 forward elimination(전방소거법)을 행렬로 코드화 한 것입니다.
엄밀하게 이야기하면 다음과 같습니다.
- L: 행렬 A를 전방소거하는데 쓰인 replacement와 scaling 에 대한 EROs를 기록해 둔 행렬
- U: 행렬 A를 전방소거한 후 남은 upper triangular matrix(상삼각행렬)
- P: 행렬 A를 전방소거하는데 쓰인 interchange에 대한 EROs를 기록해둔 행렬 (옵션)
numpy등의 모듈에서 LU 분해는 다음과 같은 return값을 지닙니다.
\(A = PLU\)
LU 분해의 활용
LU 분해는 다음의 이유로 활용됩니다.
- 수치적 안정성 : 선형시스템 $Ax = b$의 해를 역행렬 $A^{-1}$을 이용해 구하는 것보다 PLU분해를 이용하는 것이 좀 더 수치적으로 안정적입니다.
- b가 자주 업데이트 되는 경우 : 선형시스템 $Ax = b$에서 행렬 $A$는 고정되어 있고 $b$가 자주 변하는 문제가 종종 있습니다.
이런 경우, 행렬 $A$를 미리 $PLU$로 분해해 둔다면, $b$가 업데이트 될 때마다
선형시스템의 해 $x$를 실시간으로 구할 수 있습니다.위와 같은 이유로 $x = A^{-1}b$ 보다는
forward elimination과 back-substition을 이용해 x를 구하는게 더 안정적입니다.
행렬연산
행렬 관련 용어
간단하게 행렬 관련 용어를 살펴봅시다.
행렬(matrix)는 직사각형 구조에 숫자들을 담아 놓은 구조입니다.
각 숫자들은 행렬의 요소(entry)라 부릅니다.
다음과 같이 하나의 행 혹은 하나의 열을 가지는 특별한 행렬을 생각할 수 있습니다.
이들을 각각 행벡터(row vector), 열벡터(column vector)라 합니다.
극단적으로 $1 x 1$ 행렬을 생각할 수 있는데, 이는 스칼라(scalar)와 같습니다.
행렬 A의 각 (i,j)-요소는 $a_{ij}$로 나타냅니다.
행렬 A를 간략히 표기할 때는 $A=[a_{ij}]$로 나타냅니다.
행렬 A의 크기가 중요할 경우는 $A=[a_{ij}]_{mXn}$로 나타냅니다.
벡터라고 하면 일반적으로 열벡터(column vector)를 말합니다.
n-벡터는 n개의 스칼라로(scalar)로 구성된 벡터를 말합니다.
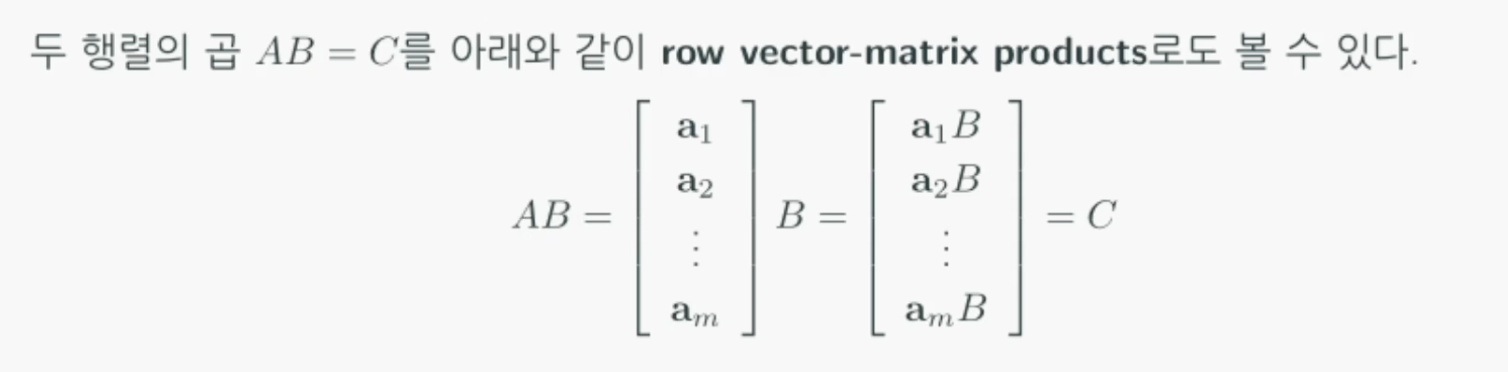
행렬의 곱
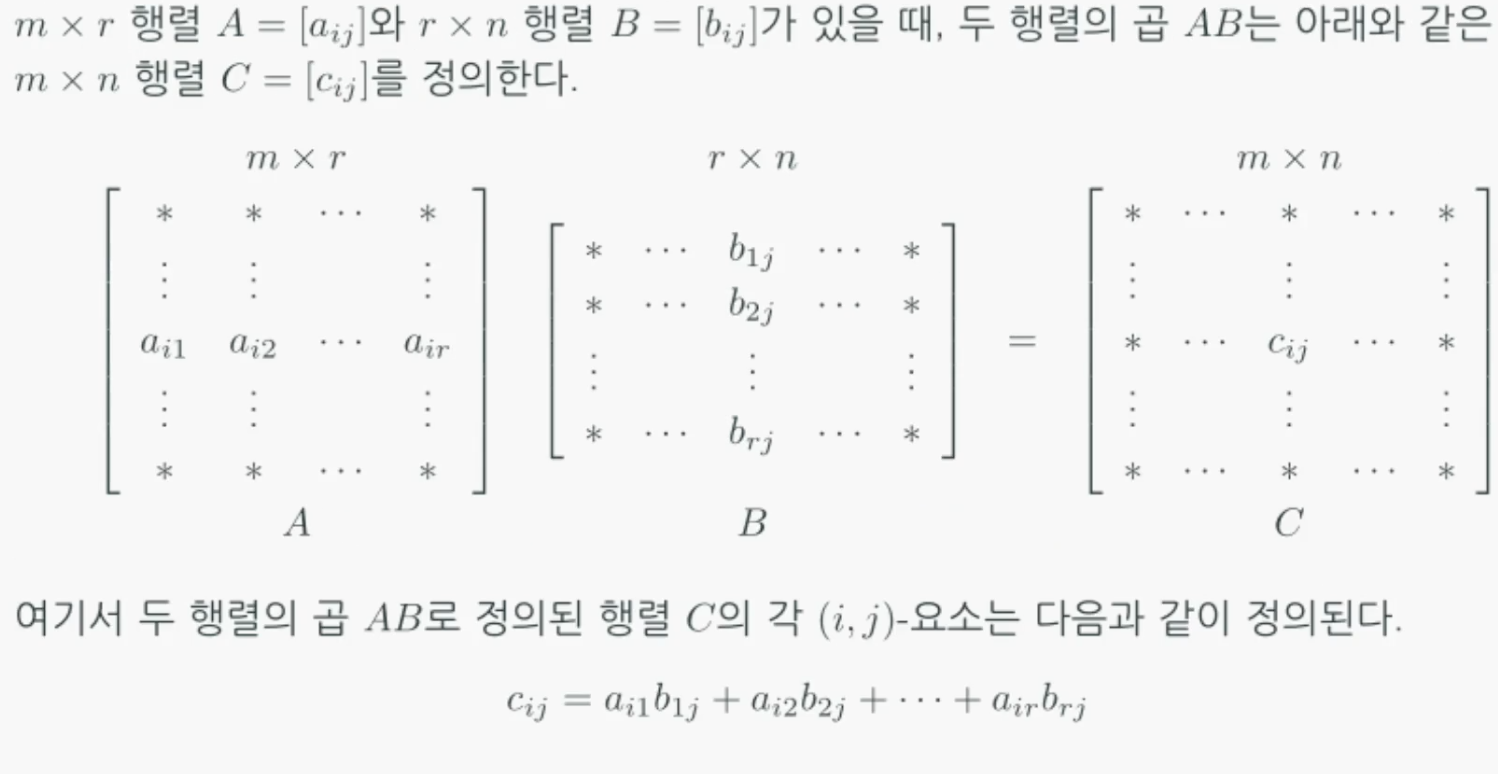
행렬의 곱으로 생겨난 요소$C_{ij}$는
좌측 행렬 A의 i행과 우측 행렬 B의 j열의 내적이라 볼 수 있습니다.
따라서 A의 열 개수와 B의 행 개수는 일치해야 합니다.
또한 행렬의 곱은 교환법칙이 성립하지 않습니다.
C의 모든 요소가 독립적이기 때문에
행렬의 곱은 병렬처리(parallel processing)로 가속할 수 있습니다.
스칼라, 벡터, 행렬, 그리고 텐서: 계층적 구조 이해하기
스칼라 -> 벡터 -> 행렬
스칼라는 숫자 하나로 구성되어 있습니다.
$7$
이 스칼라를 벡터로 표현하면 아래와 같이 1개의 구성요소로 이루어진 1-벡터가 됩니다.
$[7]$
이 스칼라를 행렬로 표현하면 아래와 같이 1개의 구성요소로 이루어진 1 X 1 행렬이 됩니다.
벡터 -> 행렬
벡터는 여러 숫자가 일열로 늘어선 구조입니다. 다음은 4-벡터의 예시입니다.
\(\begin{bmatrix}
1\\
2\\
3\\
4
\end{bmatrix}\)
이 벡터를 행렬로 표현 하면 다음과 같이 여러 모양의 행렬로 표현할 수 있습니다.

행렬 -> 벡터
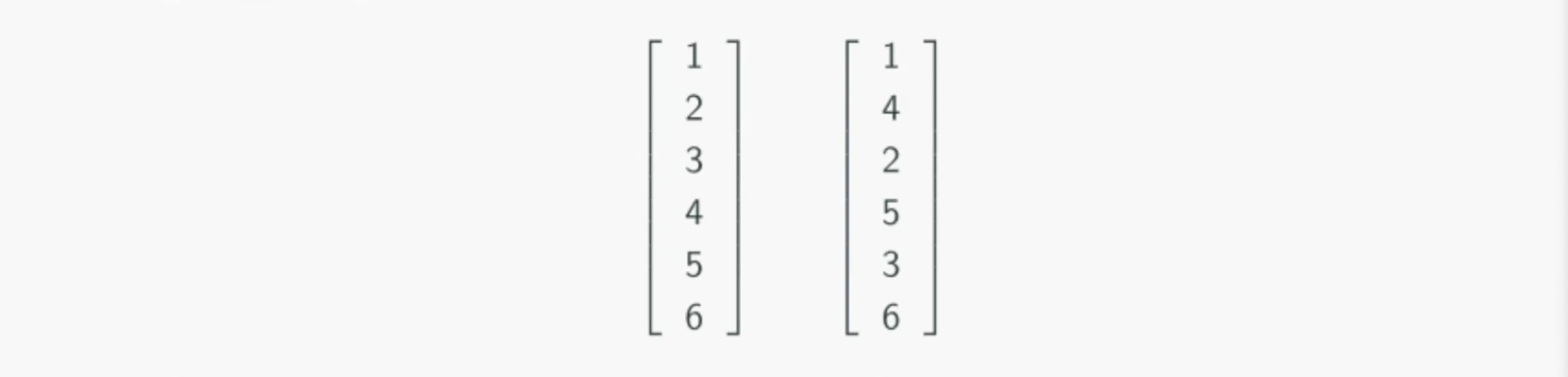
행렬은 사각형 구조에 여러 숫자가 행과 열로 늘어선 구조입니다.
\(\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6
\end{bmatrix}\)
이 행렬은 다음과 같이 6-벡터로 표현할 수 있습니다.
텐서
텐서(tenser)는 스칼라, 벡터, 행렬을 아루르는 개념입니다. 숫자가 늘어설 수 있는 방향이 k개면 k-텐서라 부릅니다.
- 0-텐서: 스칼라
- 1-텐서: 벡터
- 2-텐서: 행렬

여기서 영상데이터와 같이 시간에 따른 개념을 추가 시키면 4-텐서도 만들 수 있습니다.
분할행렬(Partitioned Matrix)
행렬을 조각(partition) 단위로 분할하여 생각해도 무방합니다.
왜냐하면 행렬끼리의 곱연산에서 부분적인 연산을 진행해도 같은 결과가 나오기 때문입니다.
행렬은 부분행렬(submatrix)로 이루어진 직사각형 구조로 확장해서 생각할 수 있습니다.
이렇게 행렬을 여러 구조로 보는 방법을 분할행렬(partition matrix) 또는 블록행렬(block matrix)이라 합니다.
분할행렬로 행렬의 곱 이해하기
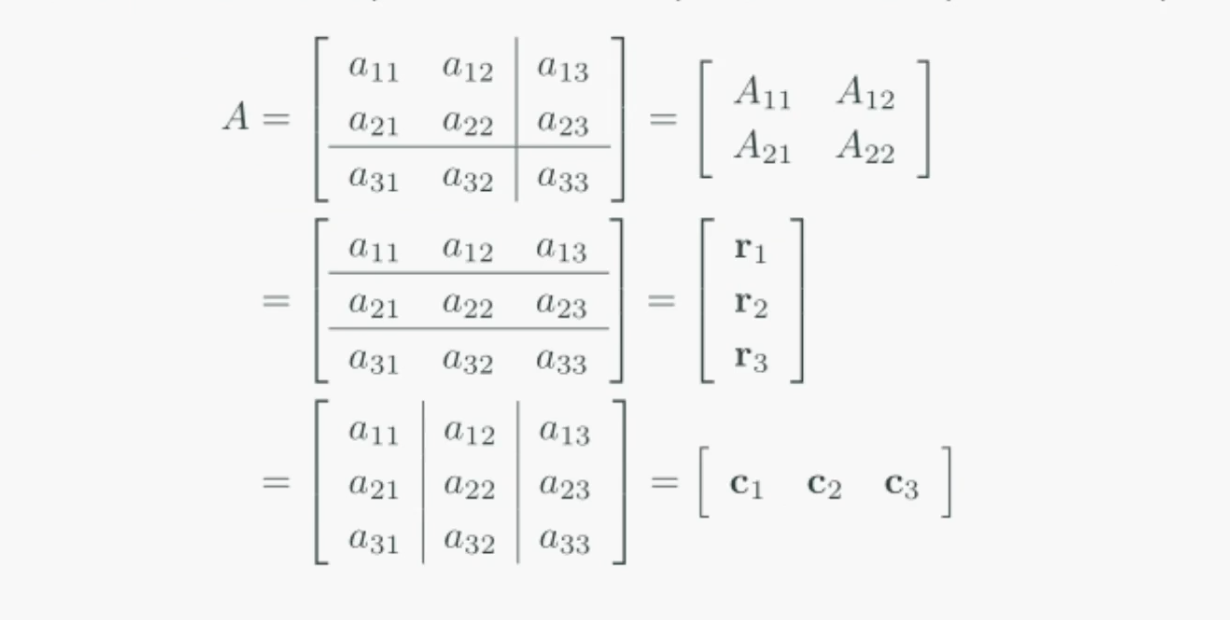
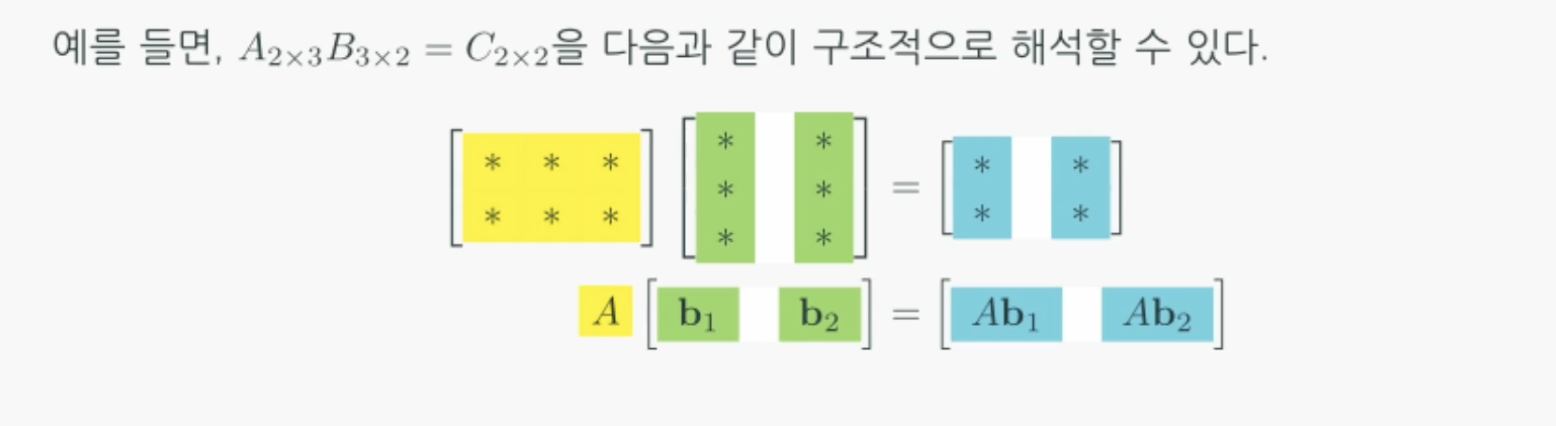
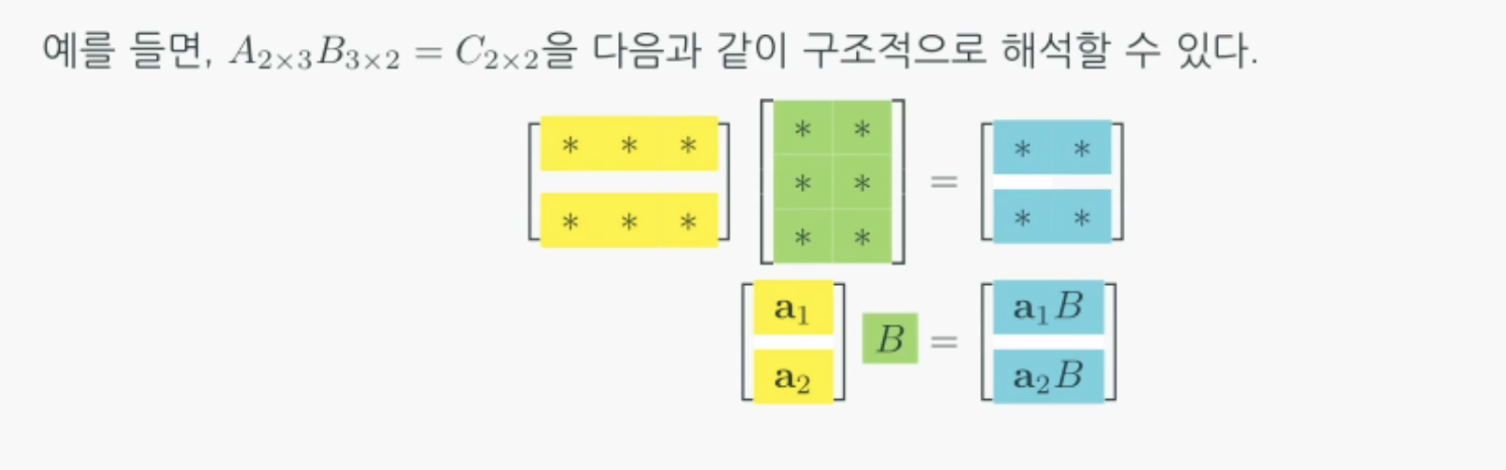
선형조합(Linear Combination)
Ax는 A의 열벡터에 대한 선형조합
행렬을 구조적으로 바라보는 가장 효과적인 방법은
행렬이 열벡터의 리스트라고 생각해보는 것입니다.
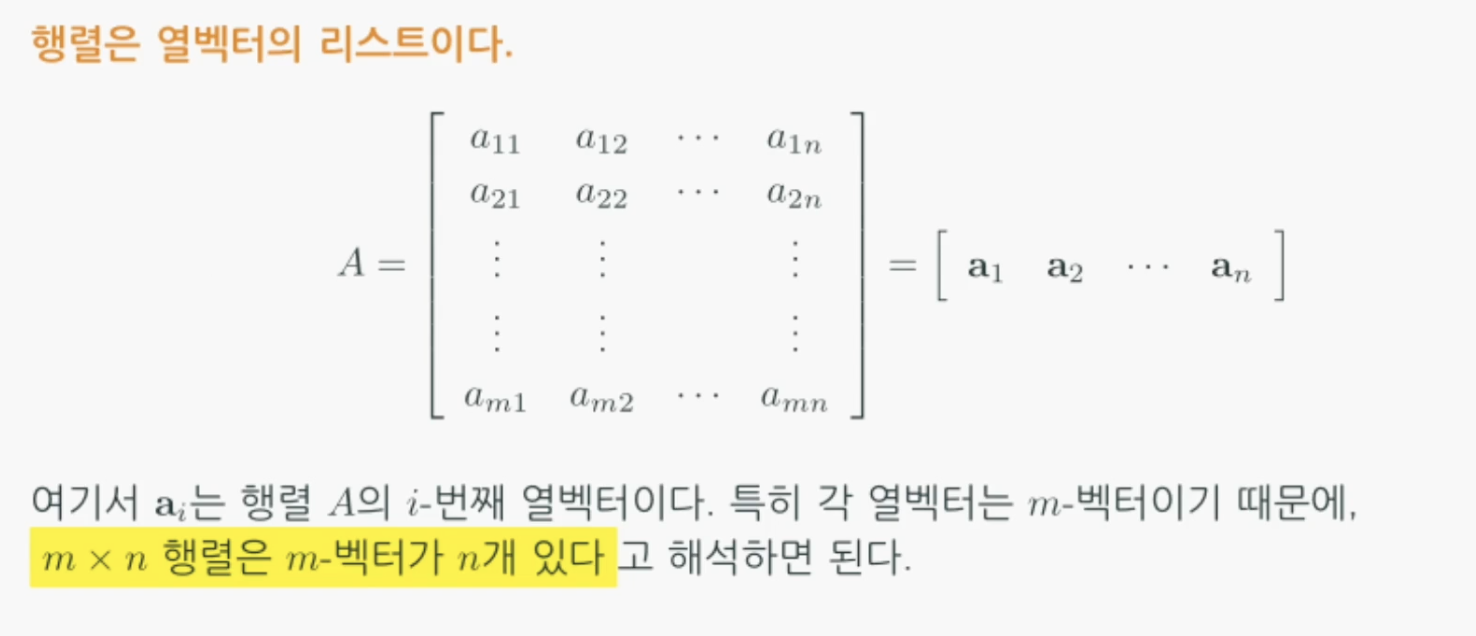
그러면 이제, Ax를 다음과 같이 볼 수 있습니다.
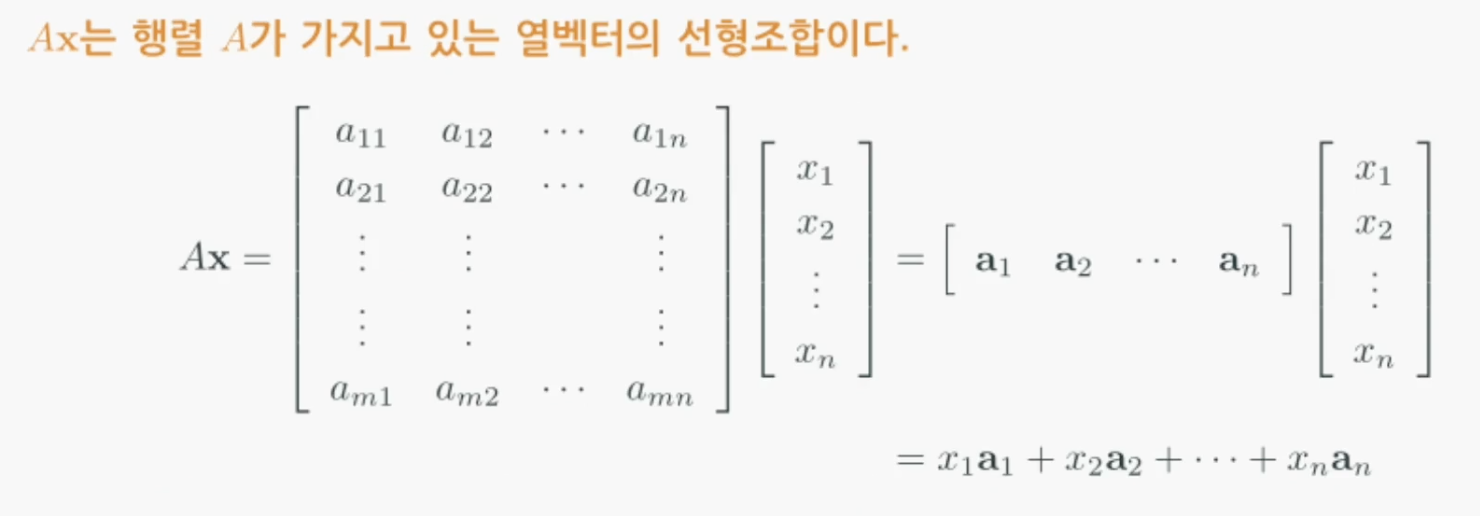
선형대수에서는 이처럼 벡터들에 대한 가중치의 합을
선형조합(linear combination)이라 부릅니다.
정리하면 다음과 같습니다.

결론적으로 선형조합 관점에서 다음과 같은 선형시스템 문제를 푼다면
좌항이 하는 이야기는 아무리 복잡해도 A의 열벡터를
가중치와 결합한 것이라 이야기 할 수 있고,
특정한 b를 만족시키는 가중치의 조합이 존재한다면
선형시스템의 해가 존재한다는 뜻입니다.

Column Space(열공간)

댓글남기기