Basic! 인공지능 수학 part 1: 선형대수

Basic! 인공지능 수학의 첫번째 시간으로 선형시스템에 대해 알아봅시다.

목표

• 선형시스템에 대한 기본적인 이해
• 가우스 소거법을 기반으로 한 선형시스템의 변수 처리

저희가 이번에 함께 알아볼 선형시스템은 여러 과학분야에서 응용되는 시스템으로,
이미지를 조합해 새로운 이미지를 만들어 내거나 (이미지 벡터의 선형조합)
특정 네트워크나 전류의 흐름을 알아낼 때에도 사용됩니다.

선형시스템의 기본적인 형태는 다음과 같이 나타낼 수 있습니다.

\[Ax = b\]

이러한 형태를 지닌 식은 중학교 교과서에서도 찾아볼 수 있는데요.
다음과 같은 일차방정식도 위의 형태를 지닌 식이라 할 수 있습니다.

\[3x = 4\]

그리고 다음과 같은 형태의 연립방정식도 선형시스템이라 할 수 있습니다.

\(3x + y = 4\)
\(x - 2y = 1\)

위와 같은 연립방정식의 경우 저희가 교과과정에서 배운 내용으로 해결할 수 있는데요.
위와 같은 식이 수천개가 넘어간다면 어떨까요?

실세계에서 응용되는 선형시스템은 저러한 수식이 굉장히 많을 수도 있고
이에 대한 변수들의 값을 모두 유추하고 싶은 경우도 있을겁니다.

그러므로 저희는 어떤 종류의 선형 시스템이던
굉장히 정형적으로 표현하고 식을 풀어낼 수 있게 만드는 것에
목표를 두고자 합니다.

아무리 복잡한 연립식이라도 $Ax = b$의 형태로 표현해서
다음과 같은 방식으로 $x$를 구해내는 것이 목표입니다.

\(Ax = b\)
\(A^{-1}Ax = A^{-1}b\)
\(x = A^{-1}b\)

선형시스템

선형 시스템의 구성요소

다음으로 살펴볼 것은 선형 시스템을 구성하는 요소들입니다.

1. 선형 방정식

• linear
  선의 형태를 나타내는 식?
  -> linear란 평면이나 왜곡되지 않은 공간(올곧은 공간)을 의미힙니다.
  ex) $3x + y + z = 4$ -> 평면 (올곧게 그려진다) -> linear하다.

• unknown(variable)
  우리가 알아내려는 미지수들을 의미합니다. ex) $x, y, z …$

\(3x + y + z = 4\)
\(x - 2y - z = 1\)
\(x + y + z = 2\)

위와 같은 시스템은 3개의 linear 시스템과 3개의 unknown으로 구성되어 있으므로
3(linear) X 3(unknown) linear system 이라 지칭할 수 있습니다.

반면 비선형 방정식이라 불리는 방정식들은 $sinx , y^3, xy$와 같이 곡선의 형태를 띄며,
변수의 승수가 1이 아닌 변수들로 구성되어 있습니다.

2. 선형시스템의 표현: $Ax = b$ (연립일차방정식의 대수적 표현)

선형방정식들을 $Ax = b$ 꼴로 표현할 수 있다면, 앞서 살펴본 것처럼 $A^{-1}$을 이용해 x를 구할 수 있을 것 입니다.

과정은 다음과 같습니다.

1. 선형시스템의 미지수들을 모아 column vector(열벡터) x로 표현합니다.
2. 선형시스템의 linear equation(선형방정식)에 대해 다음을 수행합니다.
   • coefficients(계수)를 모아 $A$의 row vector(행벡터)로 표현합니다.
   • constant(상수)를 모아 $b$에 표현합니다.

\[\begin{bmatrix} 3 & 1 & 2\\ 1 & -2 & -1\\ 1 & 1 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix} = \begin{bmatrix} 4\\ 1\\ 2 \end{bmatrix}\]

$m X n$ 선형시스템의 $Ax = b$ 표현을 정리하면 다음과 같습니다.

• 식은 행이고, 행은 식입니다.(linear equation $\leftrightarrow$ row)
• $m$은 linear equation(선형방정식)의 개수입니다.
• $n$은 unknown(미지수)의 개수입니다.
• $A$는 $m X n$ 행렬입니다.
• $x$는 $n-$벡터입니다.
• $b$는 $m-$벡터입니다.

3. 선형시스템의 해

선형시스템의 해의 종류는 3가지가 있습니다. * 해가 1개 있는 경우 (unique solution) : $3x = 6$ * 해가 없는 경우 (no solution) : $0x = 6$ * 해가 무수히 많은 경우 (infinitely many solution) : $0x = 0$

위 예시를 보면 $A = 0$이면 특이한 경우가 나오는 걸까요?
$Ax = b$ 의 해가 바로 나오지 않는 이유는
A의 역수(inverse)가 존재하지 않기 때문입니다.
위와 같은 경우를 $A$가 특이(singular)하다고 일컫습니다.

해가 존재하면 선형시스템이 consistent 하다고 하며
해가 없으면 선형시스템이 inconsistent 하다고 합니다.

가우스 소거법

가우스 소거법은 $m X n$ 선형시스템의 해를 구하는 가장 대표적인 방법입니다.
가우스 소거법은 다음의 두 단계로 수행됩니다.

1. Forward elimination(전방소거법) :
   주어진 선형시스템을 아래로 갈수록 더 단순한 형태의 선향방정식을 가지도록 변형합니다.
2. back-substition(후방대입법) : 아래서부터 위로, 미지수를 실제값으로 대체합니다.

소거법에 쓰이는 elementary row operation (EROs, 기본행연산)

다음의 행렬이 전방소거법으로 어떻게 변하는지를 보고,
기본행 연산에 대해 알아보도록 하겠습니다.

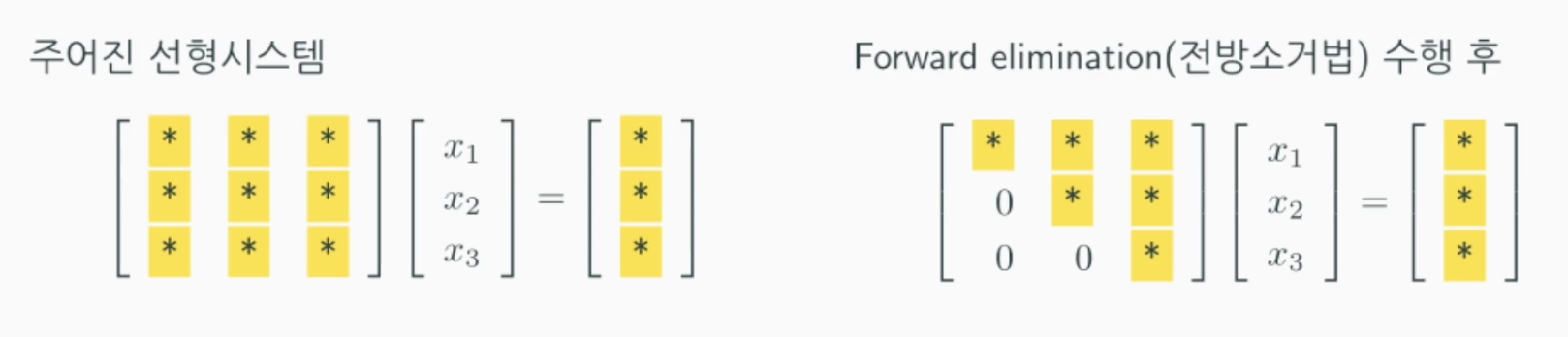
전방소거법으로 진행되는 과정은 다음과 같습니다.

각 줄에서 사용된 연산들을 기본행연산이라 부르고 그 종류는 다음과 같습니다.

Forward Elimination의 가치

Gauss elimination에서 forward elimination의 가치에 대해 알아봅시다.

• 주어진 선형시스템을 가장 풀기 쉬운 꼴(upper triangular form)로 변형해 줍니다.

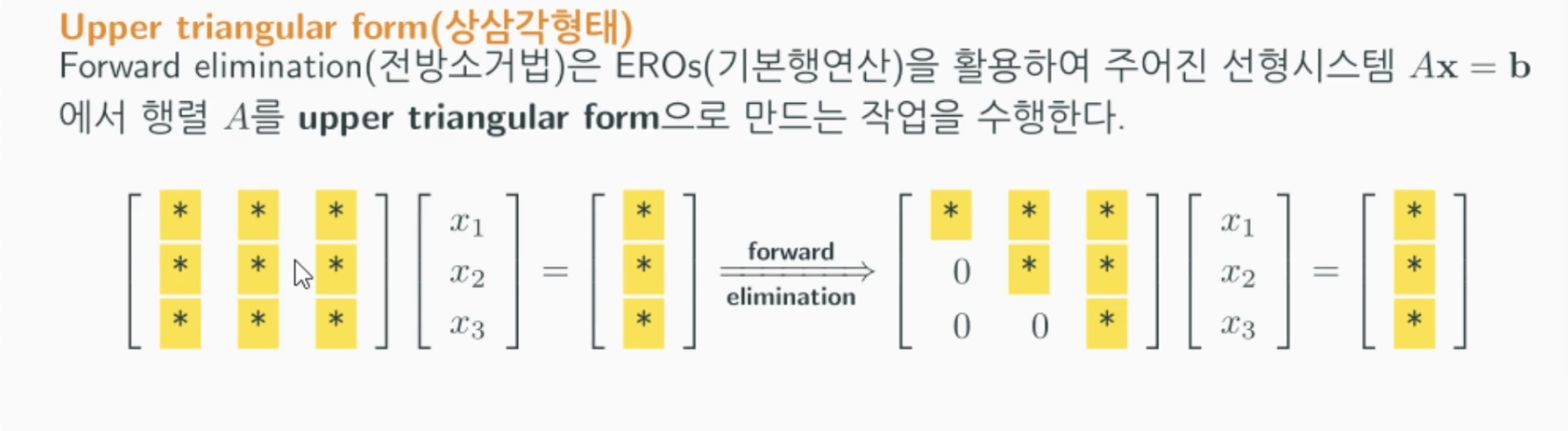
• 주어진 선형시스템의 rank(랭크)를 알려줍니다.
  rank : 의미있는 수식의 갯수

• 선형시스템이 해가 있는지 없는지 알려줍니다. (consistent vs inconsistent)