Basic! 인공지능 수학 part 3: 변환

Basic! 인공지능 수학 세번째 시간으로 좌표계 변환과 선형변환에 대해 알아보도록 합시다.

벡터

벡터의 표현

벡터는 크기와 방향을 가진 물리량으로 다음과 같이 표현될 수 있습니다.

물리적인 표현에서는 좌표계가 없고, 수학적인 표현에는 좌표계가 존재합니다.

좌표계 변환

예시를 한번 들어 보겠습니다.
i, j 좌표계에서 v = (8, 6.5)인 벡터가 존재한다고 가정해봅시다.
만일 두 벡터 $v_1$과 $v_2$를 이용해 새롭게 좌표계를 만든다면
$v$의 좌표값은 어떻게 될까요?
새로운 좌표계를 만든다는 말은 어떤 벡터 $v$에 도착하기 까지의 과정을
오롯이 $v_1$과 $v_2$를 몇번 사용해 도착했는지로 표현한다는 것과 같습니다.

즉, $v_1$과 $v_2$를 이용해 만든 새로운 좌표계에서 $v$의 좌표값은 (4,3)이 될 것입니다. 왜냐하면
\(4v_1 + 3v_2 = v\)
으로 해석이 되기 때문입니다.

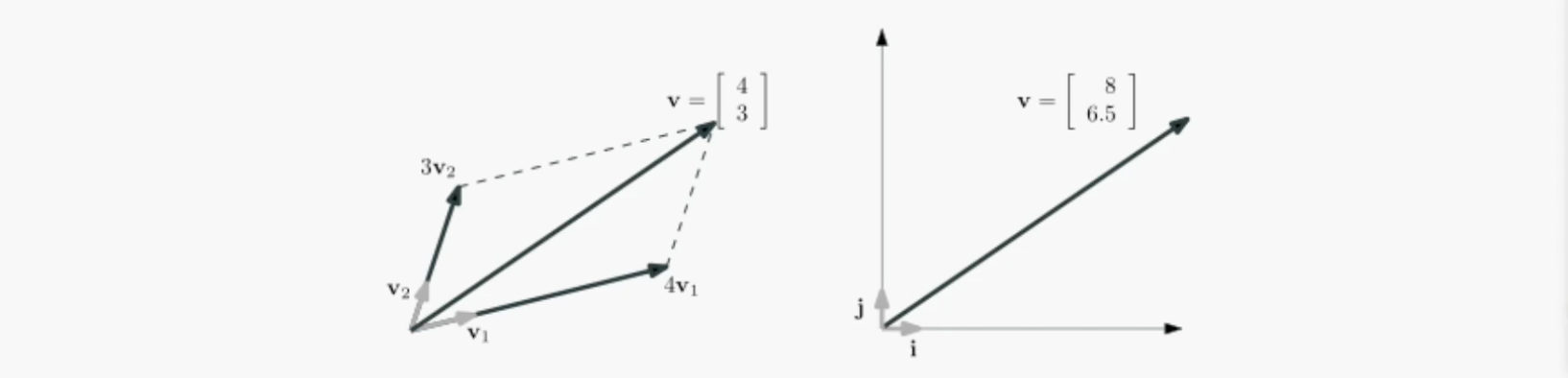
위 그림을 다른 방식으로 표현하면,
\(\begin{bmatrix} v_1 & v_2 \end{bmatrix} \begin{bmatrix} 4\\ 3 \end{bmatrix} = \begin{bmatrix} i & j \end{bmatrix} \begin{bmatrix} 8\\ 6.5 \end{bmatrix}\)
라 할 수 있습니다.

이제 선형시스템 문제를 좌표계 변환으로 바라보는 새로운 시선을 배웠습니다.
\(Ax = b\)

• 우항: 표준좌표계(standard coordinate system)에서 어떤 벡터의 좌표값은 $b$이다.
• 좌항: $A$의 열벡터들을 기저(basis)로 가지는 좌표계에서는 동일 벡터의 좌표값은 $x$이다.

\[\begin{bmatrix} 1 & -1\\ 2 & 2 \end{bmatrix} \begin{bmatrix} 2\\ 1 \end{bmatrix} = \begin{bmatrix} 1\\ 6 \end{bmatrix}\]

역행렬을 이용해 구하는 문제 역시도 좌표계 변환으로 바라볼 수 있습니다.

선형변환(Linear Transformation)

입력을 벡터로 받고 출력을 벡터로 내보내는 함수를 표현하고자 할 때
행렬로 표현이 가능하며 이를 위한 것이 선형변환입니다.

선형함수 (Linear Function)

만일 함수 $f$가 아래 두가지 조건을 만족하면 함수 f를 선형함수(linear function)라고 합니다.
\(f(x+y) = f(x) + f(y)\)
\(f(cx) = cf(x)\)
(단, $c$는 임의의 스칼라)

위 식은 언듯 보면 당연하게 보이지만, 실은 함수$f$에 대해 전혀 당연하지 않은 성질을 설명하고 있습니다.

변환

현재 선형변환에 대해 이야기 하고 있지만 대부분의 인공지능 모델은 비선형 변환을 시행한다.
그러나 행렬을 input으로 받고 행렬을 output으로 내보낸다면 일단 변환의 일종이다.

선형변환 코딩하기

행렬변환의 입출력이 벡터로 정의된 선형함수라면,
다음 절차를 통해 우리가 원하는 방식대로 동작하는 행렬변환을 코딩할 수 있습니다.

1. 구현하고자 하는 기능(function)의 입력과 출력이 벡터로 정의되는지 확인한다.
2. 구현하고자 하는 기능이 선형인지 확인한다.
3. 입력이 n-벡터이고, 출력이 m-벡터이면 $mXn$ 표준행렬(standard matrix)을 구성한다.

구하고자 하는 행렬 A의 각 열은
구현하고자 하는 기능에 각 차원의 기저벡터를 적용시킨 것과 같습니다.