[programmers][ML] 다차식에 대한 예측

머신러닝에서 목표값을 위한 식을 어떻게 추정하는지 알아봅시다.

확률이론과 결정이론

학습데이터: 입력벡터 $X = (x1,…,xn)^T$, $t = (t1,…,tn)^T$

학습의 목표: 새로운 입력 벡터가 주어졌을 때 목표값 $\hat{t}를 예측하는 것이 목표입니다.

확률이론: 예측값의 불확실성을 정량화시켜 표현할 수 있는 수학적인 프레임워크를 제공합니다.

결정이론: 확률적 표현을 바탕으로 최적의 예측을 수행할 수 있는 방법론을 평가하고 제공합니다.

A polynomial function linear in w

다차식을 피처에 대한 선형식으로 만드는 방법은 다음과 같습니다.

\[y(x,w) = w_0 + w_1x + w_2x^2 + ... + w_Mx^M = \sum_{j=0}^{M} w_jx^j\]

위와 같이 $x$에 대한 다차식을 $w$에 대한 선형식으로 나타낼 수 있습니다.

오차함수

피처를 조정하기 위해 주어진 $w$에 대한 값과 실제 데이터 $t$에 대한 오차를 구해냅니다.
오차함수는 결국 $w$에 대한 수식이라는 것을 명심합시다.

\[E(w) = 1/2 \sum_{n=1}^{N}{y(x_n,w) - t_n}^2\]

오차함수는 경우에 따라 여러가지를 사용하며 이는 원래 데이터들의 분포와 관련이 깊습니다.
이와 관련한 포스팅은 차후에 진행하도록 하겠습니다.

M 에 따른 under-fitting & over-fitting

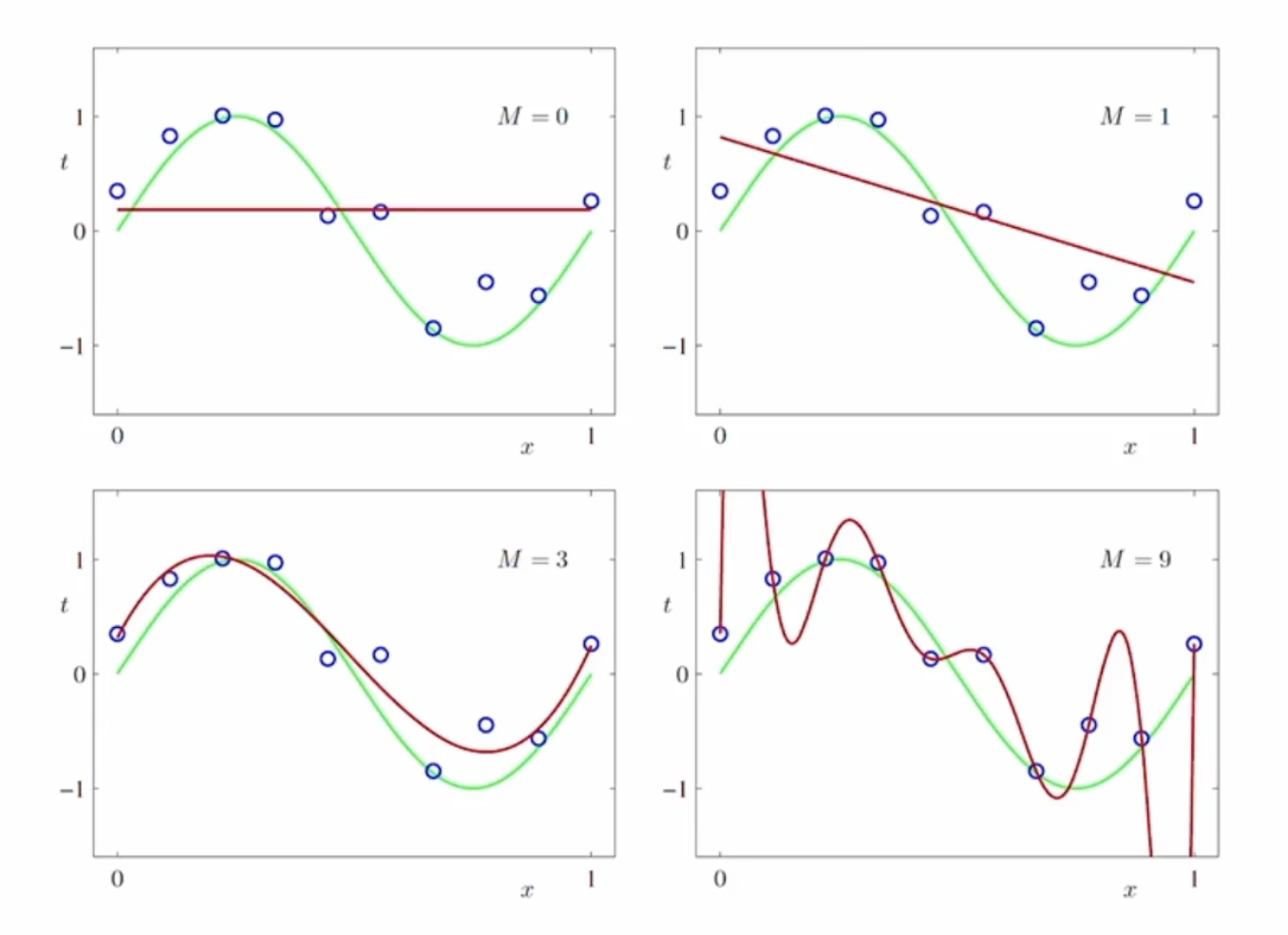
이러한 과(소/대)적합을 확인하는 방법으로는 training set과 test set을 나눠서 검증하는 방법이 있습니다.
다음은 모델을 평가할 때 사용하는 오차율 검증 함수 입니다.
전체 크기로 나눠주는 이유는 데이터의 크기에 따라 오차율의 합의 크기도 달라지기 때문에 나누는 것입니다.

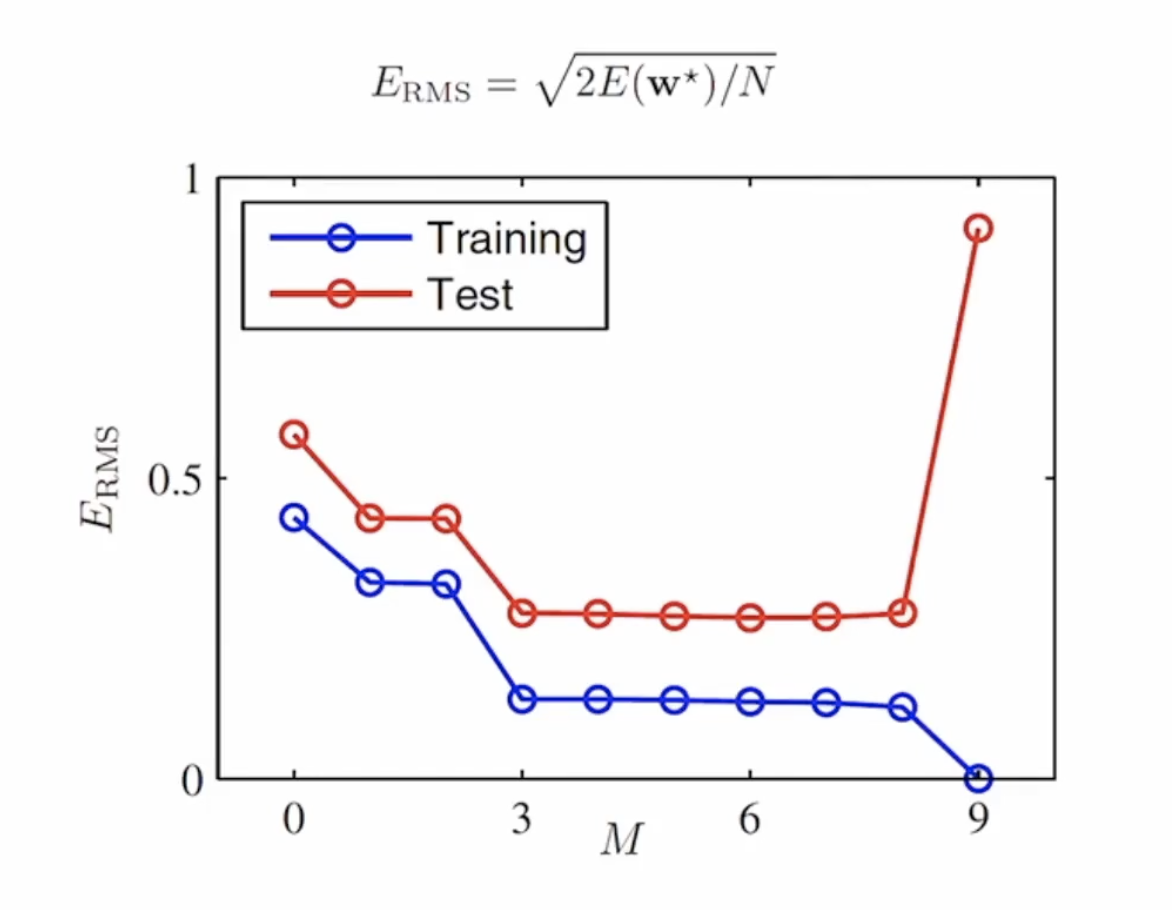
하지만 주어진 데이터의 갯수가 달라질 경우 결과가 바뀌는 것을 확인해 볼 수 있습니다.

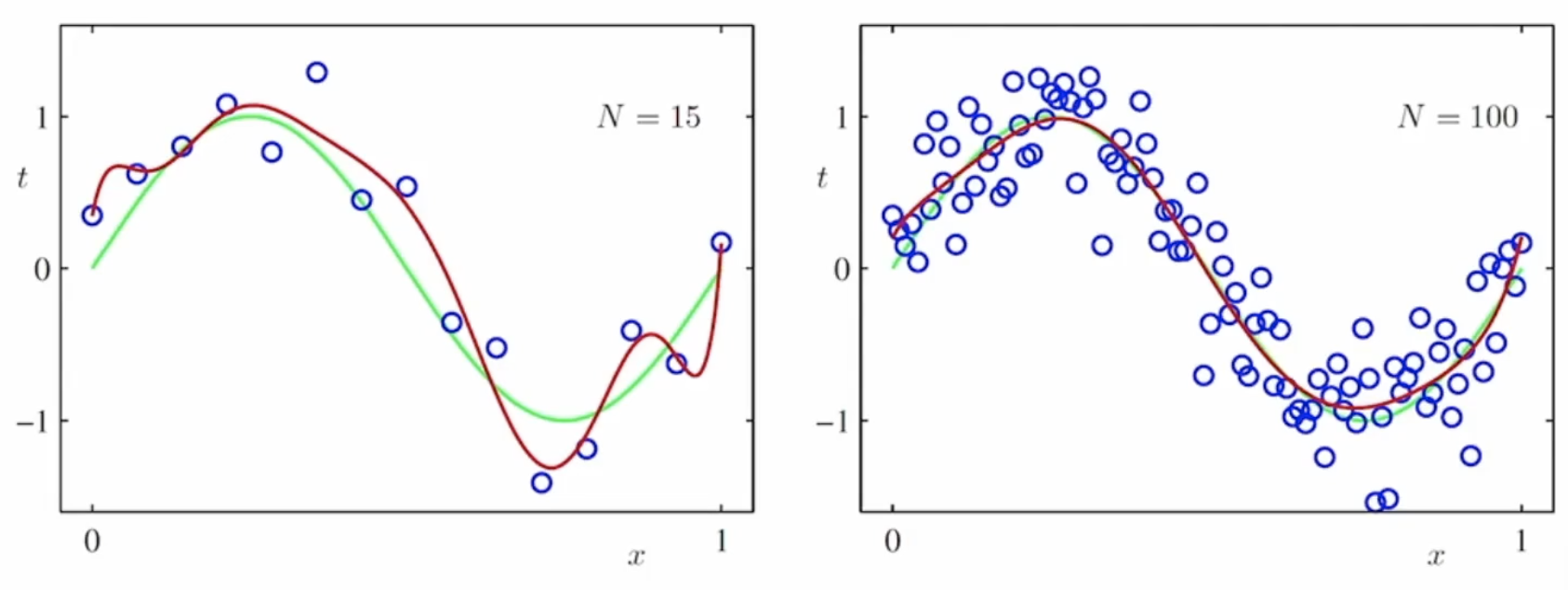
데이터가 많으면 많아질 수록 복잡한 모델을 사용할 수 있게 됩니다.

규제화 (Regularization)

M이 커질 수록 모델을 맞추기 위해 계수를 커지도록 설정하는 것을 볼 수 있습니다.
그러나 특정 계수가 너무 커지게 되면 모델의 크기가 너무 커지게 됩니다.

w에 대한 규제를 거는 방법중 대표적인 방법은 w를 인자에 집어넣어 w가 커질 수록 변동폭이 커지는 함수를 만드는 것입니다.
이 경우 람다에 대해 w가 미치는 영향을 조절할 수 있습니다.

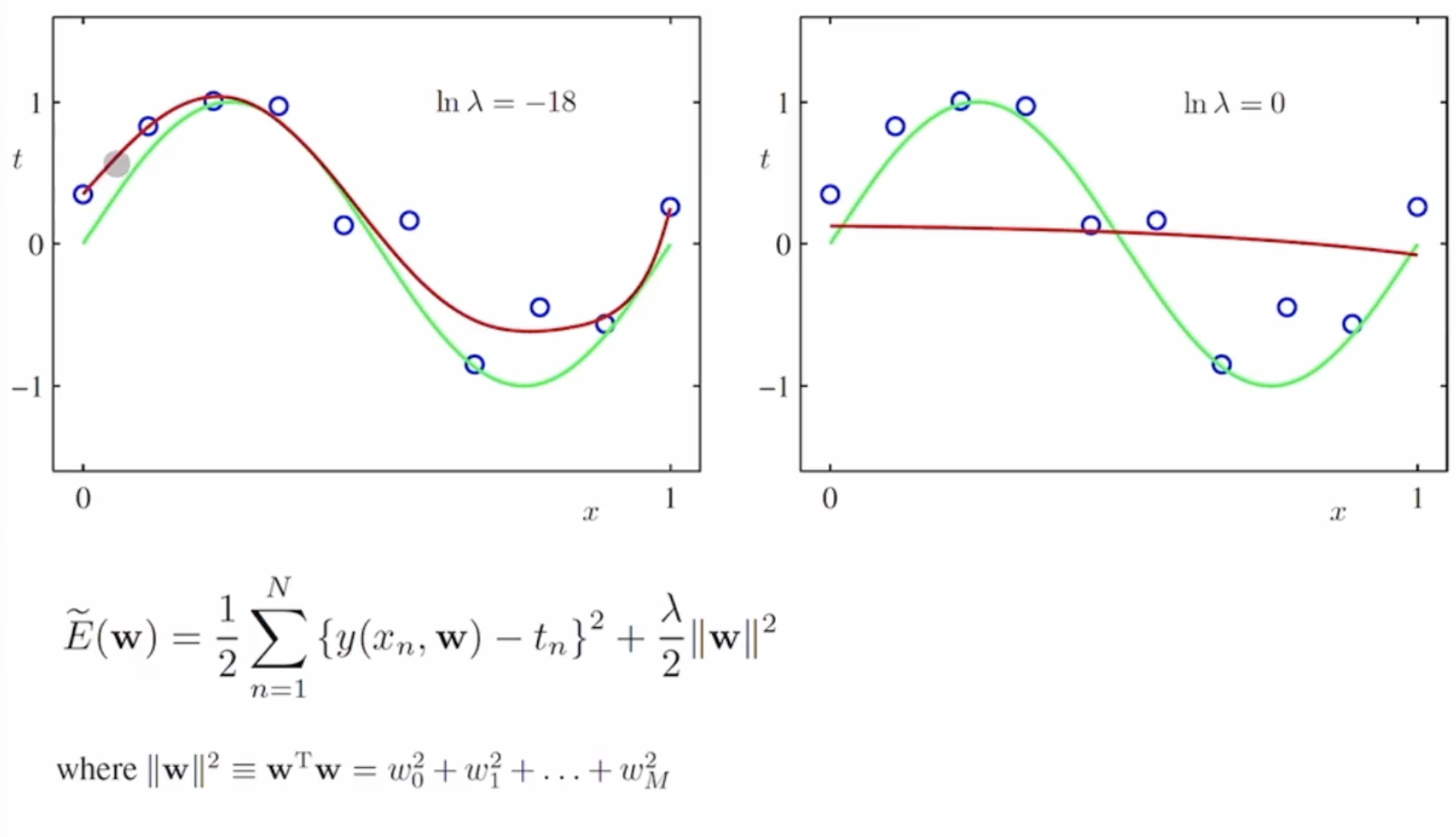
람다 값이 커질 수록 규제화가 들어가게 됩니다.
그러나 w를 너무 규제하게 되면 과소적합이 되게 됩니다.
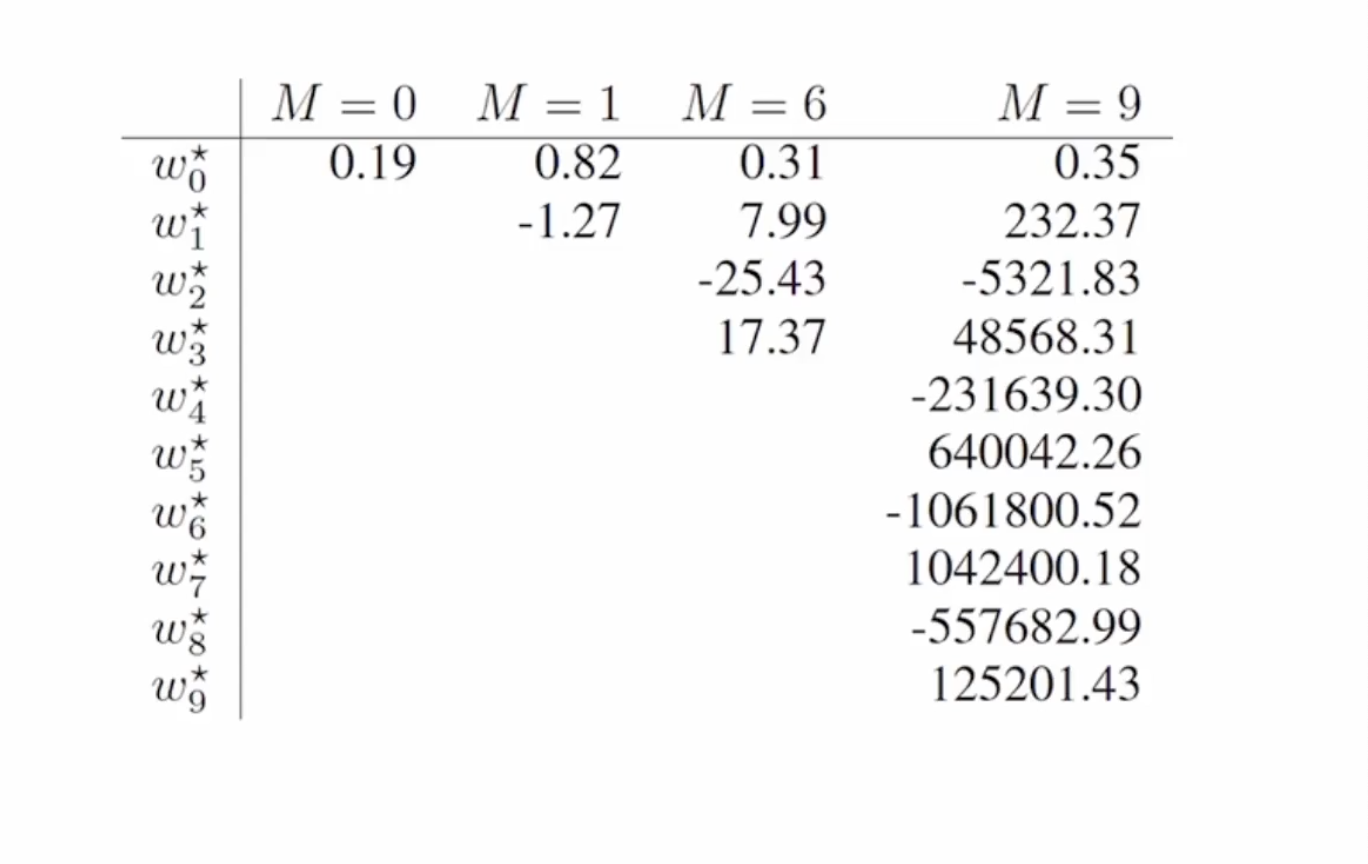
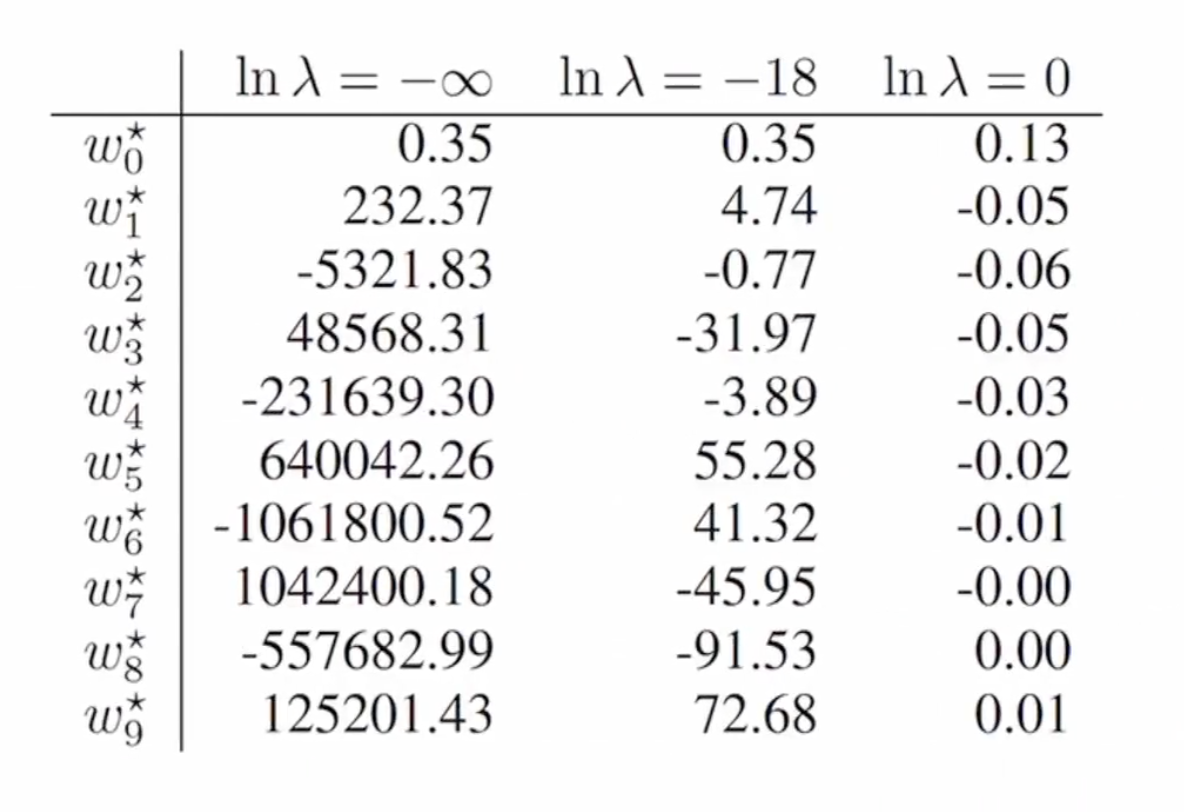
다음은 M = 9 일 때에 계수값들 입니다.