[Programmers][NLP] 문서 분류

NLP: 문서 분류

 

 

문서분류

텍스트를 입력으로 받아 텍스트가 어떤 종류의 범주에 속하는지를 구분하는 작업을 앞으로 문서분류 작업이라 정의하겠습니다.

 

문서분류의 예시

• 문서의 범주, 주제 분류
• 이메일 스팸 분류
• 감성 분류
• 언어 분류

 

ex) 감성 분류

감성의 여러 측면이 있을 수 있지만 간단한 작업에 집중하는 것이 정확한 결과를 내기 쉽습니다.

• 감성적, 태도적, 성격적 측면
• 텍스트의 긍정적인 면 vs 부정적인 면

다른 문서분류 문제들과 같이 multi class 혹은 multi label 문제로 치환될 수 있습니다.

 

문서분류의 수식적 정의

Input:

• a document d
• a fixed set of classes $C = {c_1,c_2,…,c_j}$

  Output:

• a predicted class $c$ from $C$

 

 

문서 분류 방법들

규칙 기반 모델

단어들의 조합을 사용한 규칙을 사용합니다. 블랙리스트의 아이디를 가지고 있거나 돈과 관련된 특정 내용이 있으면 스팸이라 규정하는 것처럼 사람이 규칙을 만드는 방식입니다.
사람이 만들기 때문에 특정 케이스에 대한 Precision은 높지만 조건을 모두 충족시켜 찾을 순 없으므로 recall이 낮습니다. 검출된 스팸이 진짜 스팸일 가능성은 높지만, 모든 스팸을 찾는데에는 약한 모델이라 할 수 있습니다.

 

Snorkel

각각의 규칙을 labeling function으로 간주합니다.
Graphical model의 일종인 factor graph를 사용해서 확률적 목표값을 생성하는 generative model을 사용합니다.
프로젝트 초기에 labeled data가 부족하거나 클래스 정의 자체가 애매한 경우에 매우 유용한 방법입니다. 다만, 규칙을 생성하는 것이 쉬워야 합니다.
확률적 목표값이 생성된 후에는 딥러닝 모델 등 다양한 모델을 사용할 수 있게 됩니다.

 

 

지도 학습

Input:

• a document d
• a fixed set of classes $C = {c_1,c_2,…,c_j}$
• a training set of m hand-labeled documents $(d_1,c_1),…,(d_m,c_m)$

  Output:

• a predicted class $y:d \rightarrow c$ from $C$

 

다양한 모델들

• Naive Bayes
• Logistic Legression
• Neural networks
• k-Nearest Neighbors

k-NN 을 제외한 모델은 파라미터들을 먼저 학습시켜야합니다. k-NN의 경우 주어진 문서간의 유사도를 계산한 뒤 가까운 문서들의 label이 다수인 label을 할당 시킵니다. 따라서 따로 파라미터를 학습시키지는 않습니다.

 

Naive Bayes

Bag of words

문서에 있는 단어들을 모두 추출해서 문서안에 있는 단어들의 빈도 수를 기록합니다. 이런 표현방식을 Bag of words 표현이라 합니다.
인덱스는 단어를 가리키면서 원소의 값은 빈도수를 나타내는 하나의 벡터로 문서를 표현 할 수 있습니다.

수식화

문서 d와 클래스 c 가 있다고 했을 때,
\(P(c \mid d) = \frac{P(d \mid c)P(c)}{P(d)}\)
로 표현할 수 있습니다.

이를 클래스에 대해 최대화 하는 조건은 다음과 같습니다. \(argmax P(c \mid d)\)

위 식을 c에 대한 조건부 확률로 치환할 수 있는데, P(d)는 클래스의 영향을 받지 않으므로 없애도 무방합니다.
\(= argmax P(d \mid c) P(c)\)

document d 는 각각의 n개의 속성들로 나타낼 수 있습니다.
\(P(d \mid c) = P( x_1,x_2,...,x_n \mid c)\) 이 부분이 확률의 likelihood 함수가 됩니다.
각각의 x가 가질 수 있는 가짓수 n에 대해서 exponential 한 조합이 나오게 됩니다.
데이터가 아주 크지 않으면 신뢰할 만한 정확도로 계산할 수 없기에 두 가지 가정을 통해 단순화를 시킬 필요성이 있습니다.

• Bag of words 가정:
  위치는 확률에 영향을 주지 않습니다.
• 조건부 독립 가정:
  클래스가 주어지면 속성들은 독립적입니다.

$ P(x_1, …, x_n \mid c) = P(x_1 \mid c) \bigcdot P(x_2 \mid c) \bigcdot … \bigcdot P(x_n \mid c) $

 

예제

“It was great” 라는 문장 x가 있을 때, 긍정 부정이라는 두개의 클래스로 분류를 하고자 합니다.

$P(x \mid c_1)$

$x_m = (0,…,1,…,0)^T \rightarrow one-hot encoding$

v : “it”, “was”, “great”, “bad”

각각의 단어에 해당하는 위치의 요소만 1인 sparse matrix로 문장 x를 나타낼 수 있습니다.
문장 x 는 $x_1, x_2, x_3$ 로 표현가능합니다.

$P(x \mid c_1) = \prod_{m=1}^M P(x_m \mid c_1) = P(x_1 \mid c_1) P(x_2 \mid c_1) P(x_3 \mid c_1) $

각 단어의 긍정적인 정도에 따라 전체 문장의 긍정도가 판별됩니다.
이 확률은 각 단어의 빈도수로 계산할 수 있습니다.
해당 클래스에 해당하는 문서들을 모두 모은 뒤에, 그 안에서 등장하는 특정 단어의 수를 (문서의 전체 단어의 수 + class에 해당하는 단어의)수 로 나누면 구할 수 있습니다.

 

Laplace (add-1) smoothing

특정 클래스에 없는 단어가 등장할 경우 위와같이 확률을 구한다면 확률이 0이 되어버리게 됩니다.
따라서 실제로 한번도 등장하지 않았더라도 default 등장 횟수를 1로 설정함으로써 이러한 상황을 개선할 수 있습니다.

 

지금까지의 결과를 알고리즘으로 나타내면 다음과 같습니다.

학습이 끝난다음 테스트를 진행하기 위해 다음과 같은 알고리즘을 사용합니다.

이를 통해 다음과 같은 예제를 풀어볼 수 있습니다.

 

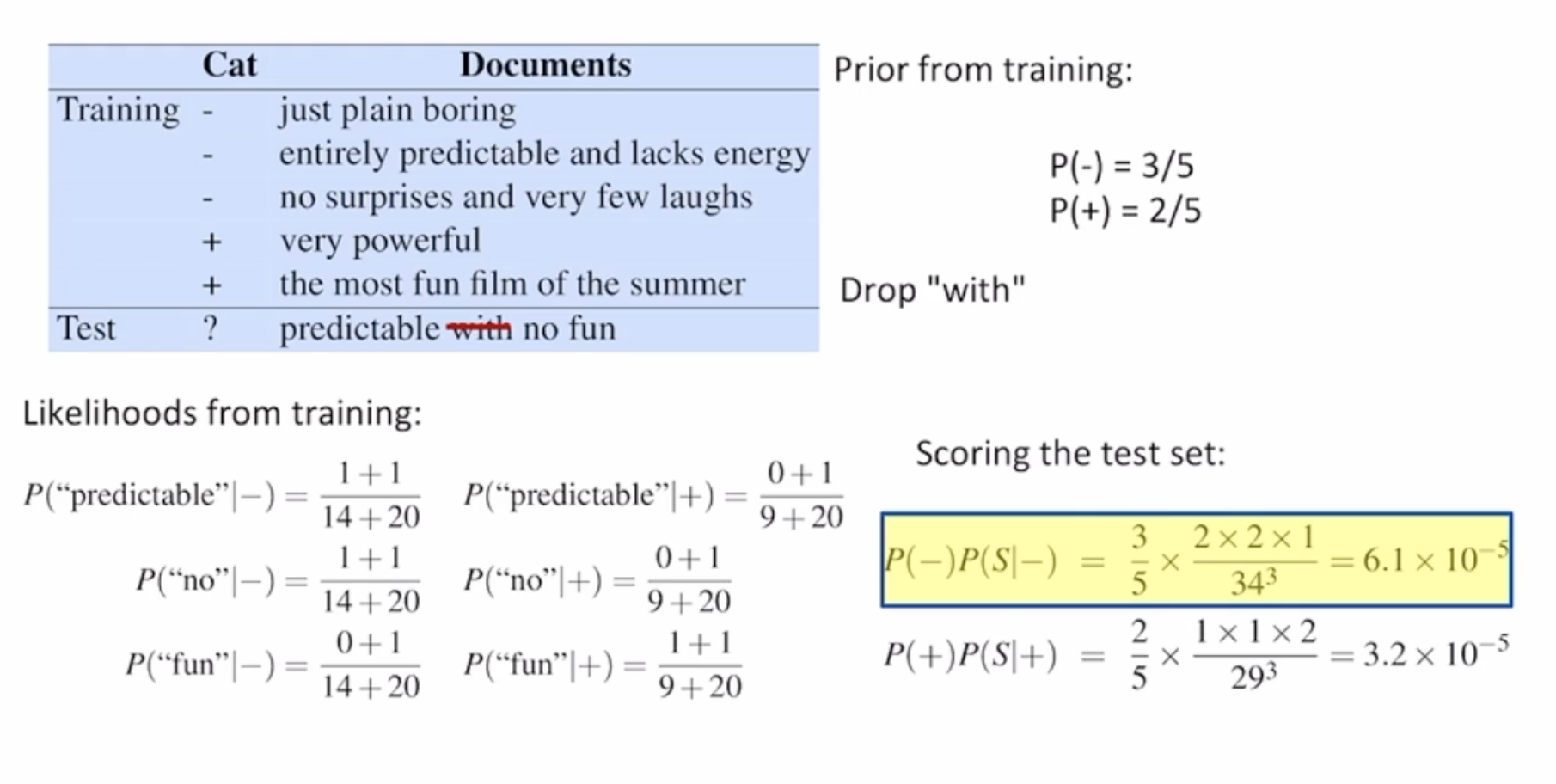
Naive Bayes 요약

• 적은 데이터로도 어느정도 좋은 성능을 보여줍니다.
• 학습과 추론 속도가 굉장히 빠릅니다.
• 조건부 독립 가정이 실제 데이터에서 성립할 때는 최적의 모델입니다.
• 문서 분류를 위한 베이스라인 모델로 적합합니다.